Andregradsfunksjoner og tredjegradsfunksjoner er to av de vanligste typene ikke-lineære funksjoner vi møter i matematikken. De skiller seg fra lineære funksjoner ved at grafene deres ikke er rette linjer, men buer som peker oppover, nedover – eller svinger flere ganger. Denne teksten vil forhåpentligvis hjelpe deg å forstå hva som kjennetegner andregrads- og tredjegradsfunksjoner, hvordan du kjenner dem igjen, og hva grafene deres faktisk forteller deg.
Hva er en andregradsfunksjon?
En andregradsfunksjon er en funksjon der x er opphøyd i to – altså der x² er den høyeste potensen av x.
Det høres kanskje avansert ut, men det betyr rett og slett at uttrykket inneholder et x²-ledd, og at det ikke finnes noen høyere eksponenter av x.
For eksempel:
f(x) = ax² + bx + c
Dette er en andregradsfunksjon, fordi x² er den største potensen av x i uttrykket.
I tillegg er a, b og c konstanter (faste tall), og a ≠ 0. Hvis a hadde vært 0, ville x²-leddet forsvunnet, og vi hadde hatt en lineær funksjon i stedet.
Slik ser grafen til en andregradsfunksjon ut
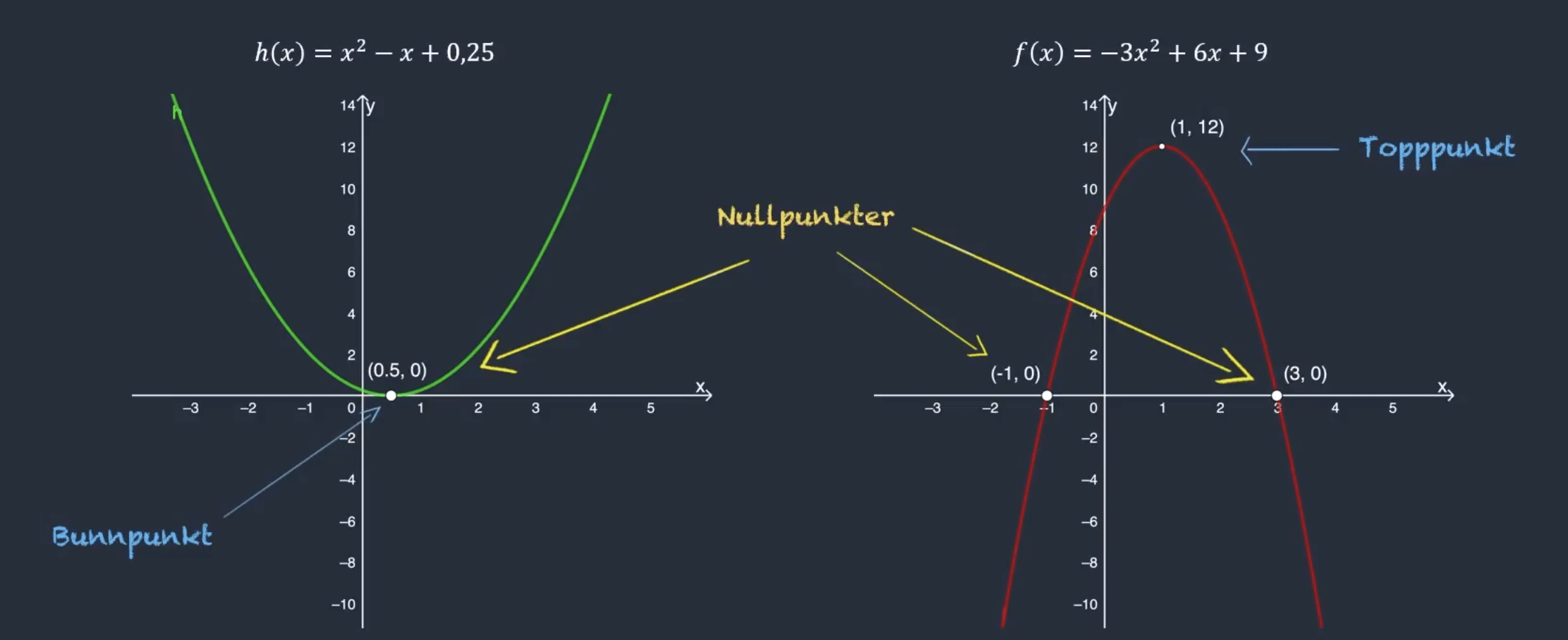
Tegner du en andregradsfunksjon i et koordinatsystem, får du en parabel – en buet graf som enten peker oppover eller nedover. Formen bestemmes av verdien til a.
- Hvis a > 0, peker buen oppover – grafen “smiler”
→ Funksjonen har et bunnpunkt - Hvis a < 0, peker buen nedover – grafen “ser sur ut”
→ Funksjonen har et toppunkt
Dette høyeste eller laveste punktet på grafen kalles et ekstremalpunkt.
Andregradsfunksjoner har alltid nøyaktig ett ekstremalpunkt – enten et toppunkt eller et bunnpunkt.

Konstantleddet – der grafen treffer y-aksen
Når vi ser på en andregradsfunksjon, for eksempel
f(x) = ax² + bx + c
er c det vi kaller konstantleddet.
Konstantleddet viser hvor grafen krysser y-aksen når x = 0. Dette punktet kalles ofte y-skjæringspunktet.
Med andre ord: Setter du inn x = 0 i funksjonen, får du verdien til c.
Eksempler:
- f(x) = x² – 3x – 1 → her er c = −1, så grafen skjærer y-aksen i y = -1.
- g(x) = 2x² − 5x → her mangler det et konstantledd, men da vet vi at c = 0, og grafen går gjennom (0, 0).
Tips: Husk at konstantleddet alltid forteller deg hvor grafen treffer y-aksen, uansett hvordan grafen ellers ser ut.
Nullpunkter og ekstremalpunkt

I en andregradsfunksjon, for eksempel
f(x) = ax² + bx + c
er nullpunktene de x-verdiene som gjør at funksjonsverdien blir 0.
Med andre ord:
Når f(x) = 0, ligger punktet på x-aksen.
Det er derfor vi sier at grafen skjærer x-aksen i nullpunktene.
Slik finner du nullpunktene
For å finne nullpunktene setter du ganske enkelt funksjonen lik null og løser likningen:
ax² + bx + c = 0
Løsningen(e) du får for x, er nullpunktene. Disse punktene forteller oss hvor grafen krysser x-aksen.
En andregradsfunksjon kan ha:
- To nullpunkter → grafen skjærer x-aksen to steder
- Ett nullpunkt → grafen tangerer (berører) x-aksen
- Ingen nullpunkter → grafen ligger helt over eller under x-aksen
Eksempler:
- f(x) = -3x² + 6x + 9 → grafen skjærer x-aksen to steder, ved x = -1 og x = 3.
- h(x) = x² – x + 0,25 → grafen har ett nullpunkt ved x = 0,5.
Husk:
Når du snakker om ekstremalpunkter (topp- eller bunnpunkt), oppgir du hele punktet (x, y).
Når du snakker om nullpunkter, oppgir du bare x-verdiene.
Hva er en tredjegradsfunksjon?
En tredjegradsfunksjon er en funksjon der x er opphøyd i tre – altså der x³er den høyeste potensen av x. Det betyr at uttrykket alltid inneholder et x³-ledd, og at det ikke finnes noen høyere eksponenter av x.
For eksempel:
f(x) = ax³− bx² + cx + d
Dette er en tredjegradsfunksjon, fordi x³ er den største potensen av x i uttrykket og a ≠ 0.
Slik ser grafen til en tredjegradsfunksjon ut illustrasjon over tredjegradsfunksjoner med piler til alle begrepene i teksten
Grafen til en tredjegradsfunksjon får ofte en bølgete form – den kan svinge opp og ned, eller gå rett gjennom uten å snu.
Hvor mye grafen bøyer seg, og i hvilken retning den går, avhenger av tallene foran leddene, altså koeffisientene.
En tredjegradsfunksjon kan ha:
- Mellom 1 og 3 nullpunkter
- Ett toppunkt og ett bunnpunkt, eller ingen ekstremalpunkter i det hele tatt.
Til sammenligning:
Hvis funksjonen i stedet hadde hatt x4 som høyeste potens – for eksempel
f(x) = 3×4− x² + 5
– da ville det vært en fjerdegradsfunksjon.

Vi har også flere andre artikler hvor du kan lære om sentrale temaer innenfor Matematikk.
Vil du lære mer om andre- og tredjegradsfunksjoner og Matematikk 1P?
Dette var bare en introduksjon til Andre- og tredjegradsfunksjoner. I vårt digitale undervisningsopplegg finner du komplette videoleksjoner, forklaringer og oppgaver som hjelper deg å forstå hele pensum. Du kan prøve faget gratis og se selv hvordan vi gjøre mattematikk 1P enklere og mer oversiktlig.
Ønsker du å lære mer? Sjekk ut våre fag og undervisning i Matematikk 1P!

MAT1019, MAT1117
Matematikk 1P – VGS

MAT1019, MAT1117
Matematikk 1P – Privatist