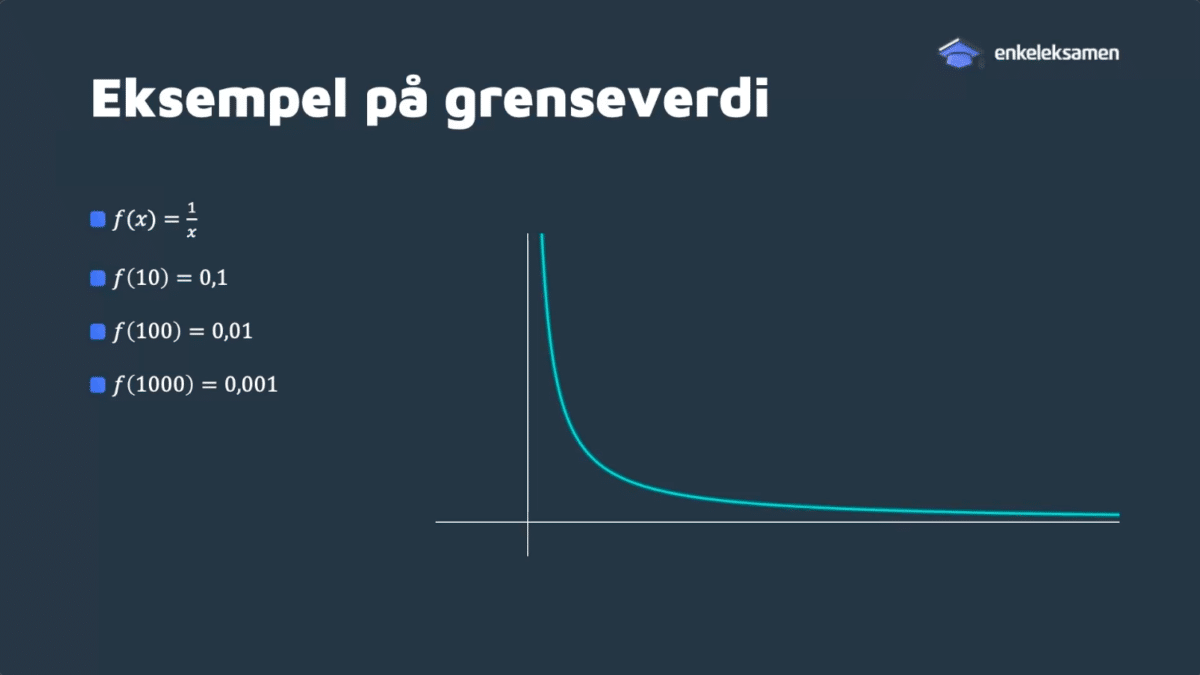
I dette innlegget skal vi introdusere grenseverdier som er et fundamentalt konsept i matematikk. Grenseverdier brukes til å beskrive hvordan en funksjon oppfører seg eller ser ut når x verdiene går mot gitte punkter. Å forstå grenseverdier er essensielt for å lære seg derivasjon og funksjonsdrøfting. Grenseverdier danner altså et viktig grunnlag for å lære seg andre aspekter av matematikken.

Hvordan ser grenseverdier ut?
Når vi skal ta grenseverdien av en funksjon ser det slik ut f(x) , hvor
- f(x) er formelen vi undersøker
- x er den uavhengige variabelen i funksjonen f(x). Dette er verdien som kan endres og som vi undersøker grenseverdien for.
- a er den verdien som x nærmer seg. Vi undersøker hva som skjer med f(x) når x blir veldig nær denne verdien.
- “lim” står for “limit” eller “grenseverdi” på norsk. Dette betegner prosessen der vi ser på oppførselen til en funksjon f(x) når x nærmer seg en bestemt verdi a.
Når vi ser på f(x) , er vi interessert i å finne ut hva verdien av funksjonen f(x) nærmer seg når x nærmer seg a. Dette gir oss en forståelse av funksjonens oppførsel i nærheten av punktet x=a.
Dette forklarer vi enda mer om her!
Eksempel på hvordan man beregner grenseverdier
La oss bruke funksjonen f(x)=x2+2x+3 som eksempel.
Vi skal finne denne grenseverdien f(x) . Vi setter da inn 2 for x i funksjonen og får:
f(x) =22+2∙2+3=11
Svaret er da at når x går mot 2, så går funksjonsverdien f(x) mot 11. Det er viktig å merke seg at x går mot 2 ikke til 2 og f(x) går mot 11 ikke til 11.
Grenseverdier ovenfra og nedenfra
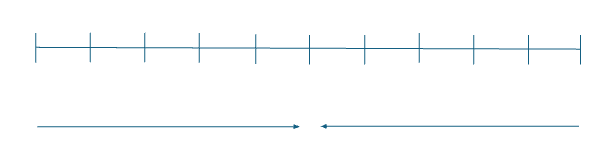
Noen ganger er det nødvendig å vurdere grenseverdier fra bare én side, enten fra ovenfra (høyre side) eller nedenfra (venstre side). Måten vi skiller oven- og nedenfra er med at ovenfra så har vi det plusstegn over tallet x går mot og for nedenfra har du et minustegn over tallet x går mot. Her ser du et eksempel:

Som du ser på tallinjen, når x går mot 0 nedenfra går x fra verdier som er lavere enn 0 mot 0. Og når x går mot 0 ovenfra så går x fra verdier som er større enn 0 mot 0.
Her ser du hva som skjer med funksjonen når x går mot null nedenfra.
| x | -1 | -0,1 | -0,01 | -0,001 | -0,0001 |
| f(x) | -1 | -10 | -100 | -1000 | -10 000 |
Og her ser du hva som skjer med funksjonen når x går mot null ovenfra.
| x | 0,0001 | -0,001 | 0,01 | 0,1 | 1 |
| f(x) | 10 000 | 1000 | 100 | 10 | 1 |
Vi ser da at når x går mot null nedefra så går verdien av funksjonen mot -∞ og når x går mot null ovenfra går funksjonen mot.
For å lære mer om grenseverdier og funksjoner, kan du finne lærerike eksamenskurs i S1 utviklet av toppstudenter nedenfor!