I denne teksten forklarer statistikkbegrepet standardavvik, hva det er, hvordan du regner det ut, og hvordan du kan bruke det til å tolke variasjon i data på en enkel og forståelig måte.
Hva betyr «standardavvik»?
La oss begynne med ordet i seg selv.
Standard betyr noe som er vanlig eller typisk, mens avvik handler om hvor mye noe skiller seg fra noe annet – i dette tilfellet gjennomsnittet.
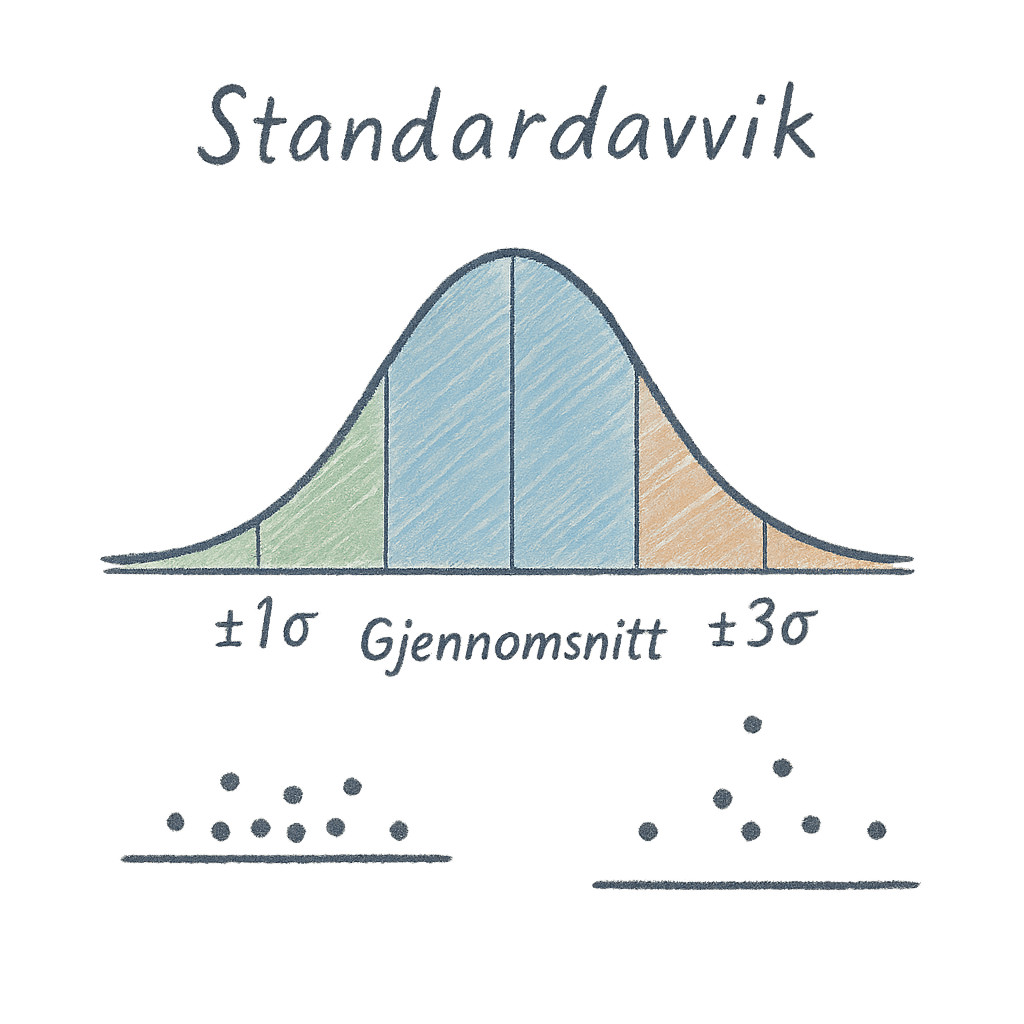
Standardavvik forteller oss altså hvor mye tallene i et datasett i gjennomsnitt avviker fra gjennomsnittet. Det er et mål på spredning, og sier noe om hvor stabile eller varierende observasjonene våre er.
Standardavvik og varians – hva er forskjellen?
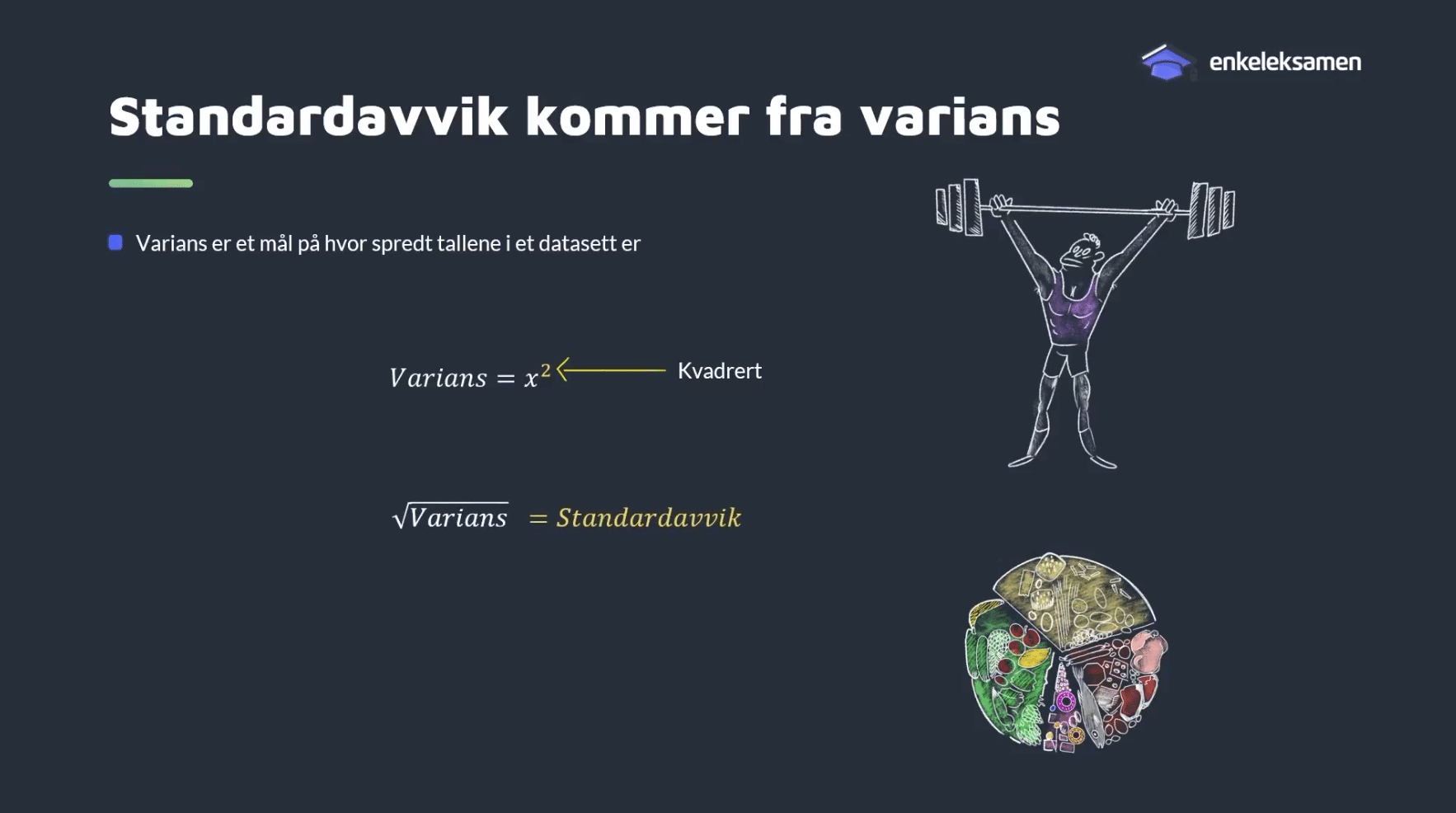
For å forstå hva standardavvik betyr, må vi først snakke litt om varians.
Du har kanskje hørt ordet variasjon før – for eksempel når vi sier at noen har et variert kosthold eller en variert treningsrutine. Det betyr rett og slett at det er forskjeller mellom ting. I statistikk betyr varians akkurat det samme: den forteller oss hvor mye tallene i et datasett sprer seg.
Men variansen kan være litt vanskelig å tolke, fordi vi bruker kvadrerte tall i beregningen – altså tall som er ganget med seg selv. Det gjør at variansen ofte får en litt «rar» størrelse.
For å gjøre tallet mer forståelig, tar vi kvadratroten av variansen. Da får vi et mål som ligger på samme skala som de opprinnelige tallene.
Dette tallet kaller vi standardavviket.
Kort sagt:
- Varians viser hvor mye tallene sprer seg.
- Standardavvik er bare en mer «lesbar» versjon av variansen.
Slik regner du ut varians og standardavvik – eksempel
La oss se på et konkret eksempel for å forstå hva standardavvik egentlig betyr.
Tenk deg at vi følger to håndballspillere, Anna og Julie, gjennom en sesong. Begge spiller 10 kamper, og begge scorer i gjennomsnitt 4 mål per kamp. Men fordelingen av målene er litt forskjellig:
| Anna | 3 | 4 | 5 | 4 | 3 | 4 | 6 | 4 | 3 | 4 |
| Julie | 0 | 2 | 8 | 4 | 6 | 1 | 7 | 3 | 6 | 3 |
Begge spillerne scorer altså i snitt 4 mål, men det ser ut som Julie varierer mer fra kamp til kamp enn Anna gjør. La oss sjekke om det stemmer – ved å regne ut varians og standardavvik.
Steg 1: Finn gjennomsnittet
Vi starter med å finne gjennomsnittet (eller «snittet»).
Anna har totalt 40 mål fordelt på 10 kamper:
40 ÷ 10 = 4 mål per kamp
Julie har også 40 mål på 10 kamper, så hun har det samme gjennomsnittet:
4 mål per kamp
Steg 2: Finn avviket fra gjennomsnittet
Nå skal vi se hvor mye hver kamp skiller seg fra gjennomsnittet.
Anna:
(3−4), (4−4), (5−4), (4−4), (3−4), (4−4), (6−4), (4−4), (3−4), (4−4)
For å slippe negative tall, kvadrerer vi avvikene (altså ganger dem med seg selv):
1², 0², 1², 0², 1², 0², 2², 0², 1², 0² → 1 + 0 + 1 + 0 + 1 + 0 + 4 + 0 + 1 + 0 = 8
Julie:
(0−4), (2−4), (8−4), (4−4), (6−4), (1−4), (7−4), (3−4), (6−4), (3−4)
Kvadrerte avvik:
16 + 4 + 16 + 0 + 4 + 9 + 9 + 1 + 4 + 1 = 64
Steg 3: Finn variansen
Nå finner vi gjennomsnittet av de kvadrerte avvikene:
Anna: 8 ÷ 10 = 0,8
Julie: 64 ÷ 10 = 6,4
Dette er variansene.
Steg 4: Finn standardavviket
Til slutt tar vi kvadratroten av variansen for å finne standardavviket:
- Anna: √0,8 = 0,89
- Julie: √6,4 = 2,53
Hva forteller dette oss?
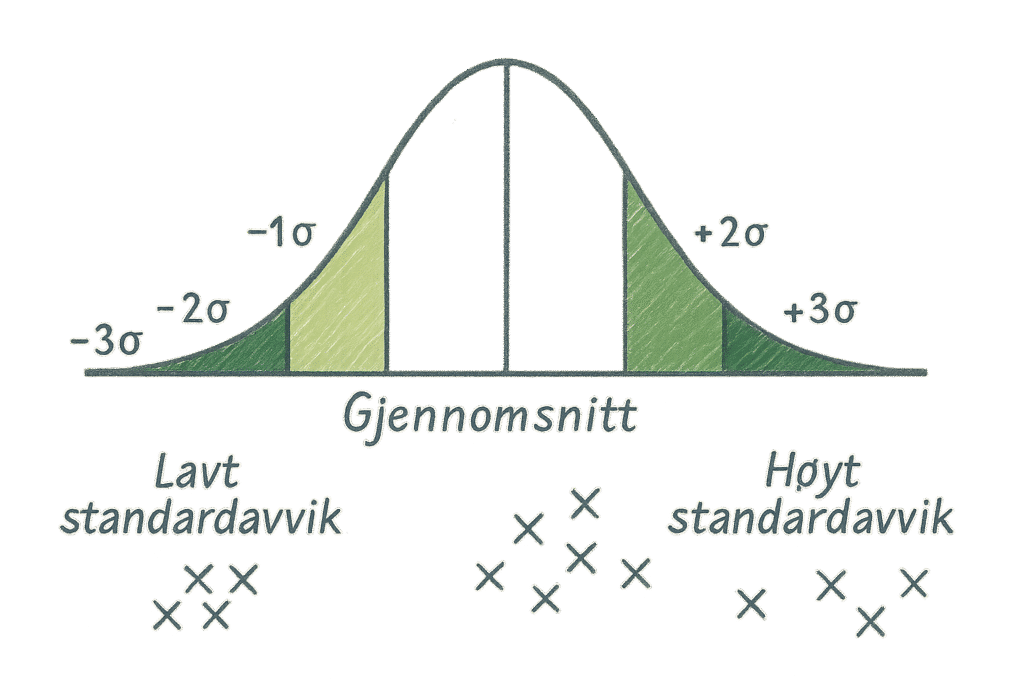
Begge spillerne scorer i gjennomsnitt 4 mål per kamp, men Anna har lavt standardavvik, mens Julie har høyt standardavvik.
Det betyr at Anna er jevn og stabil – hun scorer omtrent like mange mål i hver kamp.
Julie, derimot, er mer uforutsigbar – hun kan ha toppkamper med 8 mål og svake kamper med 0 mål.
Standardavvik hjelper oss altså å forstå hvor mye observasjonene varierer rundt gjennomsnittet.
Det gir et mer presist bilde enn bare å se på gjennomsnittet alene – enten vi snakker om håndballmål, eksamensresultater eller økonomiske data.
Vi har også flere andre artikler hvor du kan lære om sentrale temaer innenfor faget Matematikk 2P.

Vil du lære mer om standardavvik og Matematikk 2P?
Dette var bare en introduksjon til standardavvik og hvordan den fungerer. I vårt digitale undervisningsopplegg finner du komplette videoleksjoner, forklaringer og oppgaver som hjelper deg å forstå hele pensum. Du kan prøve faget gratis og se selv hvordan vi gjøre matematikk 2P enklere og mer oversiktlig.
Ønsker du å lære mer? Sjekk ut våre fag og undervisning i Matematikk 2P!

MAT1023, MAT1151
Matematikk 2P – VGS

MAT1023, MAT1151
Matematikk 2P – Privatist