Hva er skalaegenskaper?

Skalaegenskaper, også kjent som skalautbytte, forteller om hvor mye produksjonen til en bedrift øker som følge av å øke bruken av alle innsatsfaktorene. Anta at en bedrift produserer et gitt antall brød en dag. Neste dag dobler de bruken av ingredienser, noe som fører til at de vil få en fordobling i antall produserte brød. Her ser vi dermed at en fordobling av innsatsfaktorer, fører til en fordobling i produksjonsmengde.

La oss anta at vi har en produktfunksjon gitt ved

Produktfunksjonen forteller at produksjonen, y, avhenger av produktiviteten A, og innsatsfaktoren v. Eksponenten til innsatsfaktoren, gitt ved a, avgjør hvilke skalaegenskaper produktfunksjonen har. Det finnes tre ulike situasjoner for skalautbytte:

• Konstant skalautbytte
• Tiltagende skalautbytte
• Avtagende skalautbytte

Konstant skalautbytte

Under konstant skalautbytte vil en dobling av innsatsfaktoren føre til en nøyaktig dobling i produksjonen. Vi kan se at en produktfunksjon har konstant skalautbytte ved at eksponenten til innsatsfaktoren er lik 1.

Eksempel

Vi har en gitt produktfunksjon

I dette tilfellet er eksponenten til innsatsfaktoren v=1, noe som tilsier at produktfunksjonen har konstant skalautbytte. En dobling av innsatsfaktoren v vil føre til en nøyaktig dobling i produksjonen y.

Under konstant skalautbytte vil produktfunksjonen være lineær i et diagram med produksjonen y på y-aksen, og innsatsfaktoren v på x-aksen.

Tiltagende skalautbytte

Tiltagende skalautbytte tilsier at en dobling av innsatsfaktoren vil føre til mer enn en dobling i produksjonen. Vi kan se at en produktfunksjon har tiltagende skalautbytte ved at eksponenten til innsatsfaktoren er større enn 1.

Eksempel

Vi har en gitt produktfunksjon

I dette tilfellet er eksponenten til innsatsfaktoren v>1, noe som gir produktfunksjonen et tiltagende skalautbytte. En dobling av innsatsfaktoren v, vil føre til mer enn en dobling i produksjonen y.

Under tiltagende skalautbytte vil produktfunksjonen være konveks i et diagram med produksjonen y på y-aksen, og innsatsfaktoren v på x-aksen.

Avtagende skalautbytte

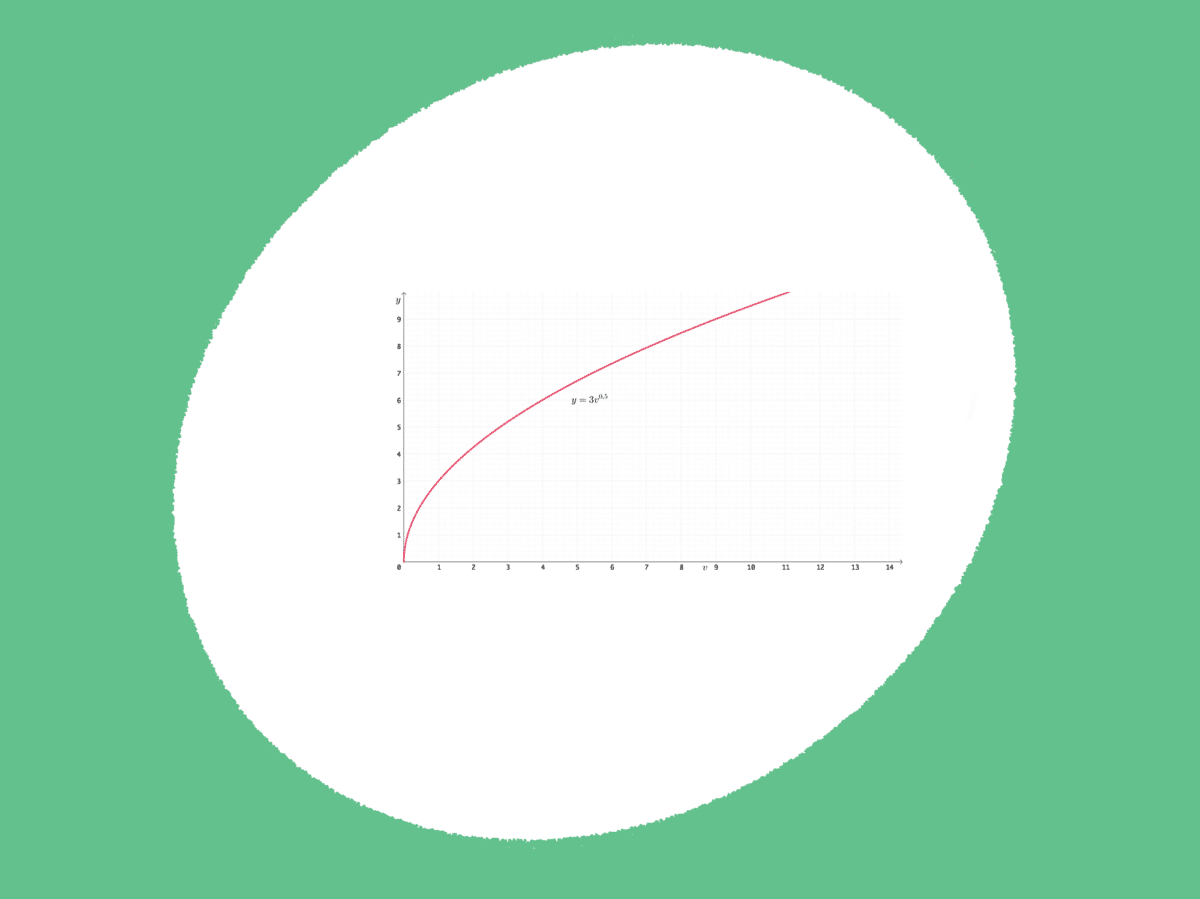
Et avtagende skalautbytte forteller at en dobling i bruken av innsatsfaktoren vil føre til mindre enn en dobling i produksjonen. Vi kan se at en produktfunksjonen har avtagende skalautbytte ved at eksponenten til innsatsfaktoren er mindre enn 1.

Eksempel

Vi har en gitt produktfunksjon

Her ser vi at eksponenten til innsatsfaktoren v<1, slik at produktfunksjonen har et avtagende skalautbytte. En dobling av innsatsfaktoren v, vil føre til mindre enn en dobling i produksjonen y.

Under avtagende skalautbytte vil produktfunksjonen være konkav i et diagram med produksjonen y på y-aksen, og innsatsfaktoren v på x-aksen.

Dersom du ønsker å lære mer om skalaegenskaper, kan du sjekke ut denne videoen. Her kan du også lære om sammenhengen mellom skalaegenskaper, marginalkostnader og grenseproduktivitet.