Varians og standardavvik for et utvalg

Studerer du Statistikk og lurer på hva varians og standardavvik er for noe? Da er du kommet til rett sted! I dette blogginnlegget vil du lære om hva varians og standardavvik for et utvalg er for noe, og hvordan du kan regne det ut.

Hva er varians og standardavvik for et utvalg?

For å vite hva varians og standardavvik for et utvalg er for noe, må vi først forklare hva et utvalg er. Et utvalg er rett og slett noen utvalgte objekter eller tall fra en populasjon/gruppe. Et enkelt eksempel er å velge 8 tilfeldige studenter ved NTNU og spørre dem hvor mange timer i uka de ser på serier. Tallene de svarer er utvalget vårt, og dette kan vi bruke til å finne varians og standardavvik for utvalget. Dette kalles også empirisk varians og empirisk standardavvik (empirisk = «erfaringsmessig»).

La oss si de 8 studentene svarer:

9

5

7

8

4

7

6

3

De fleste av tallene ligger rundt 6 og det er ingen som ser veldig mye eller veldig lite på serier. Det er altså litt variasjon i tallene, men ikke veldig mye.
La oss heller si at de 8 studentene svarer:

10

4

8

9

0

15

6

2

I dette tilfellet er det mye større variasjon, og det er tall helt fra 0 til 15. For å forklare variasjon i hverdagen så fungerer utrykkene “stor variasjon” og “lite variasjon” helt greit. I statistikk derimot, er det ofte behov for å sette tall på hvor stor denne variasjonen er. Til dette brukes begrepene varians og standardavvik!

Regne ut varians

Utvalgsvarians kalles ofte for $S^2$. Formelen for å regne det ut er

I denne formelen så er

• $n$ antall tall i utvalget, og kalles ofte antall observasjoner
• $x_i$ er hvert av tallene, altså hver observasjon
• $\bar{x}$ er gjennomsnittet av alle observasjonene

Eksempel 1

I det første eksempelet fra i stad svarte de 8 studentene
9, 5, 7, 8, 4, 7, 6, 3
La oss regne ut variansen for dette utvalget. Først så må vi finne gjennomsnittet $\bar{x}$:

Før vi regne ut variansen, så kan vi studere dette i et koordinatsystem. Hver av de 8 observasjonene er plassert i et koordinatsystem, og gjennomsnittet er den blå linjen. Det som summeres opp i variansen er avstanden mellom observasjonene og linjen for gjennomsnittet, opphøyd i andre.

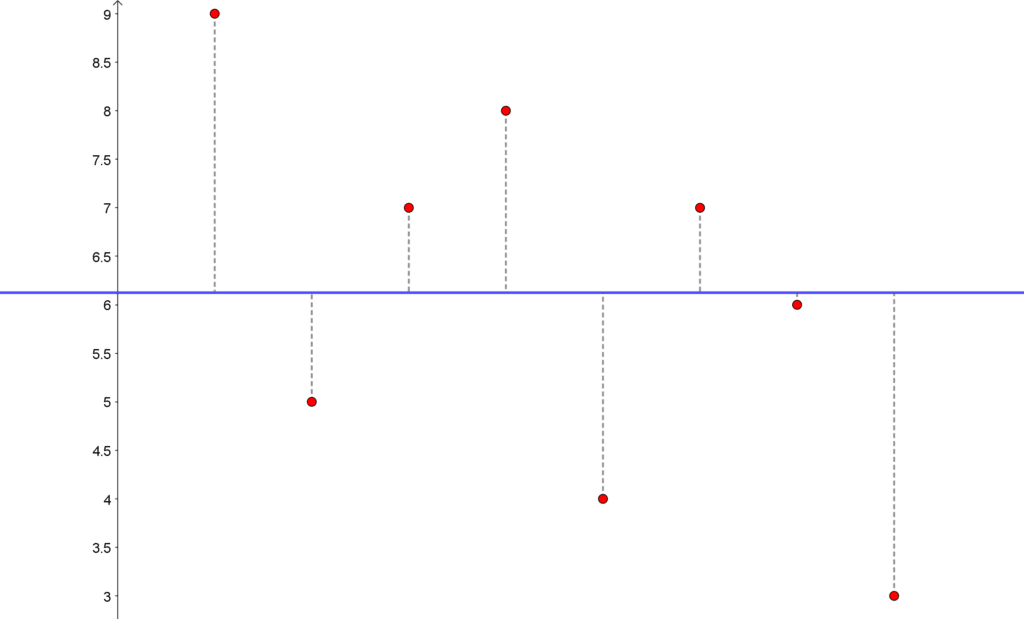
Nå er det bare å regne ut variansen:

Den empiriske variansen, eller variansen til utvalget, er altså 4,125.
La oss se hva den blir i det andre tilfellet.

Eksempel 2

De alternative svarene fra de 8 studentene var
10, 4, 8, 9, 0, 15, 6, 2
La oss regne ut variansen for dette utvalget. Først så må vi igjen finne gjennomsnittet $\bar{x}$:

Vi kan skissere dette grafisk igjen, og hvis man ser på de to grafene er det tydelig at avstandene mellom gjennomsnittet og observasjonene er mye større i dette eksempelet, og dermed blir variansen også mye større!

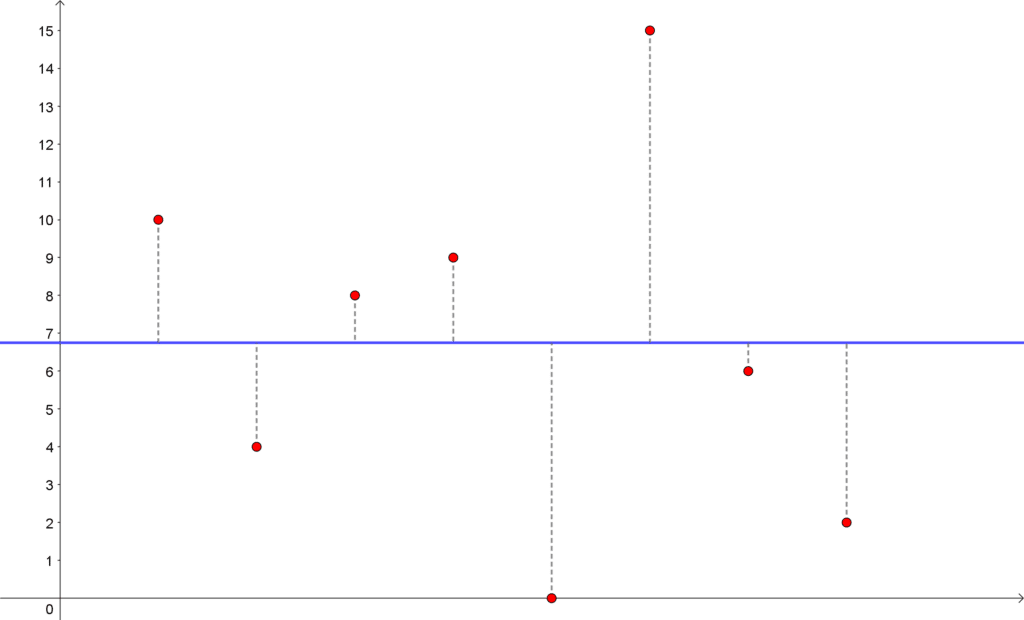
Gjennomsnittet er ikke så langt fra hva det var i eksempel 1, men la oss se hva variansen blir:

Variansen i dette tilfellet er mye større!

Benevning for varians

Når variansen regnes ut så bruker man kvadratet (opphøyd i 2) av differansen mellom observasjoner ($x_i$) og gjennomsnitt ($\bar{x}$). Siden det er opphøyd i to blir også benevningen til variansen opphøyd i 2. I disse eksemplene ser vi på antall timer studenter bruker på serier. Benevningen til tallene i utvalget er altså timer. Benevningen til variansen er derfor timer². I siste eksempelet er variansen $23,071~timer^2$. Timer opphøyd i 2 gir lite mening, men heldigvis så har man utrykket standardavvik der dette problemet forsvinner.

Regne ut standardavvik

Det å regne ut standardavviket er veldig lett hvis du allerede har regnet ut variansen. Definisjonen av et utvalgs standardavvik er

Standardavviket er kvadratroten av variansen, og dermed blir benevningen til standardavvik det samme som benevningen til utvalget vårt (f.eks. timer). En annen måte å definere standardavviket er: Gjennomsnittlig avvik fra gjennomsnittet.
Når variansen regnes ut så tar man avviket mellom observasjoner og gjennomsnitt og opphøyer i andre, for alle observasjonene. Siden standardavviket er kvadratroten av variansen, så blir dette det gjennomsnittlige avviket for alle observasjonene.

Med mindre man får oppgitt variansen, så er det ingen måte å regne ut standardavviket uten å først regne ut variansen og deretter ta kvadratroten av dette. La oss se på hva standardavviket er i de to tidligere eksemplene.

Eksempel 1

I det første eksempelet fra i stad svarte de 8 studentene
9, 5, 7, 8, 4, 7, 6, 3
Variansen til dette utvalget er $S^2=4,125$.
Standardavviket er

Eksempel 2

I det andre eksempelet fra i stad svarte studentene
10, 4, 8, 9, 0, 15, 6, 2
Variansen fant vi at er $S^2=23,071$.
Standardavviket er

Notasjon for varians og standardavvik

I dette blogginnlegget har vi brukt notasjonene

• Empirisk varians: $S^2$
• Empirisk standardavvik: $S$

Hvilken notasjon som brukes varierer litt, og noen bruker små s-er slik som dette:

• Empirisk varians: $s^2$
• Empirisk standardavvik: $s$

Med subskript_x,y

I noen tilfeller har du kanskje en rekke observasjoner kalt $x_i$ og noen andre kalt $y_i$. Hvis du skal regne ut variansen til x-ene og y-ene er det lurt å skille mellom hvilken $S^2$ som tilhører $x$ og hvilken som tilhører $y$. Da brukes ofte en subskript på variansen og standardavviket. For $x$ ville man i så fall skrevet noe som dette

• Empirisk varians: $S^2_x$
• Empirisk standardavvik: $S_x$

Varians og standardavvik for en stokastisk variabel

I forbindelse med statistikk har du kanskje hørt om stokastiske variabler? I så fall er det naturlig å møte på utrykkene:

• $Var[X]$
• $Std[X]$

Dette er henholdsvis varians og standardavvik til en stokastisk variabel $X$. Disse størrelse er noe annet enn $S^2$ og $S$. Du kan lære mer om slike stokastiske variabler og deres varians i våre statistikk-kurs på enkeleksamen.no.

På enkeleksamen.no finner du en rekke fag i Statistikk og Statistikk for økonomer tilpasset skoler og universiteter rundt om i Norge. I kursene har du mulighet til å se videoer, gjøre quizzer og få hjelp av våre supre nettlærere!