Se for deg et koordinatsystem med mange punkter. Hvordan finner du da en rett linje som passer med alle punktene i koordinatsystemet? Hvordan vet man om linjen passer bra eller ikke? Hva er egentlig lineær regresjon?
I denne teksten vil vi prøve å besvare disse spørsmålene, men hvis du ønsker en dypere innføring i dette emnet kan du gå til enkeleksamen.no og sjekke ut våre kurs i statistikk.
Hva er lineær regresjon?
Ofte vil du møte datasett med en såkalt lineær sammenheng. Med datasett menes det altså en rekke punkter: (x1, y1), (x2, y2), …, (xn, yn). Enkelt forklart så betyr lineær sammenheng at hvis du tegner punktene fra datasettet i et koordinatsystem, så vil de ligge på en tilnærmet rett linje. På bildene under ser du forskjellen mellom lineær sammenheng (til venstre), og to andre datasett der det ikke er noen lineær sammenheng. Det kan altså ikke tilpasses noen rett linje som passer godt med alle punktene i de to figurene til høyre.
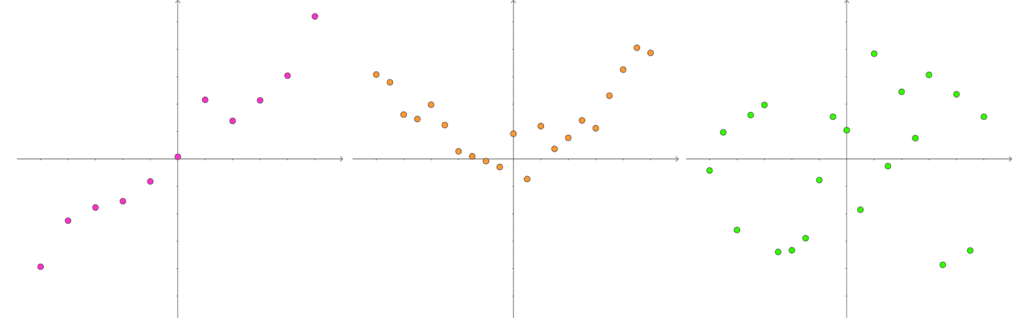
Finn linjen som passer best
Lineær regresjon handler om å finne en rett linje som passer best mulig med alle punktene. Som vist i figuren under så kan det være flere linjer som passer ganske godt med punktene i et datasett, men det er den grønne som passer aller best!
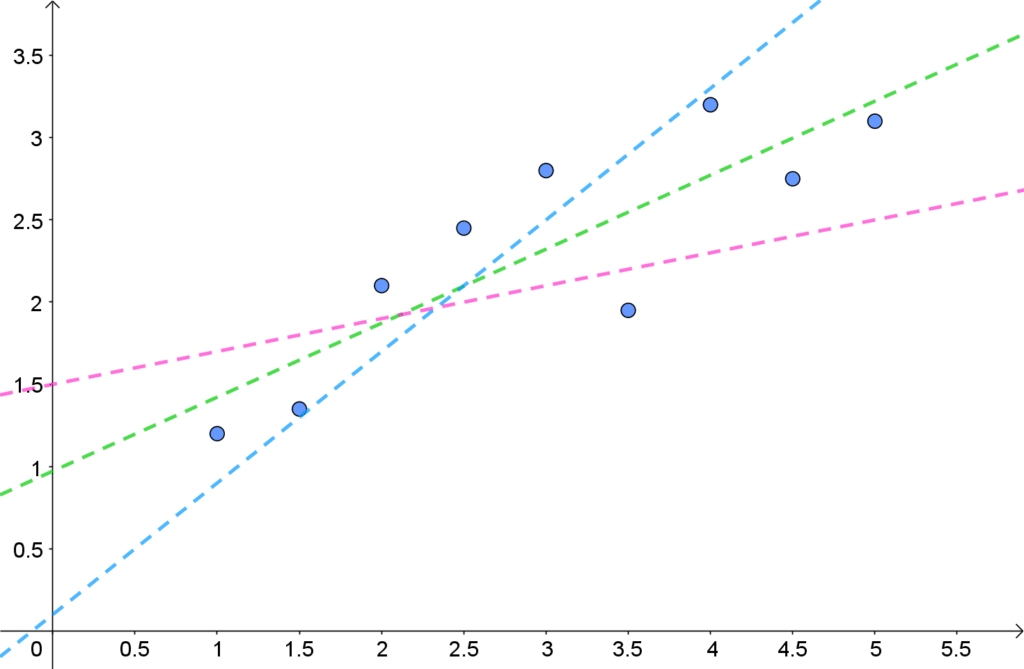
Minste kvadraters metode
Som nevnt tidligere er poenget med lineær regresjon å finne den best tilpassede. Måten vi gjør dette er ved å bruke minste kvadraters metode. Poenget med denne metoden er at hvis en linje går langs alle punktene, vil vi kunne regne ut feilen mellom verdien linjen gir og den ekte verdien i punktet, altså feilen mellom predikert og observert y-verdi. Alle de observerte punktene i datasettet er (x1, y1), (x2, y2), …, (xn, yn). En rett linje er skrevet på formen:
y = \alpha x + \beta
Her er α og β henholdsvis stigningstall og konstantledd. Dersom punktene i datasettet nesten ligger på en rett linje, så kan vi beskrive hver y-verdi i datasettet ved hjelp av en forklaringsvariabel x og en feil ε (epsilon) som tar høyde for avviket.
Vi har da:
y_i=\alpha x_i + \beta+\epsilon_i
for alle i = 1, 2, …, n. Aviket εi er altså avviket mellom et punkt i et datasett og selve linja. Problemet er at vi ikke kjenner til α og β, så disse må vi prøve å estimere. Minste kvadraters metode går ut på å finne et estimat for denne linjen, som minimerer feilen for alle punktene i datasettet.
Vi bruker denne metoden til å predikere, altså anslå, en linje gitt ved:
\hat{y}=\hat{\alpha}x+\hat{\beta}«Hattene» over variablene og koeffisientene viser at disse er estimerte verdier. Derfor kalles α og β med hatter over, for regresjonskoeffisienter.
Hva er minste kvadraters metode?
La oss se nærmere på det første punktet i koordinatsystemet, sammen med den grønne linjen.
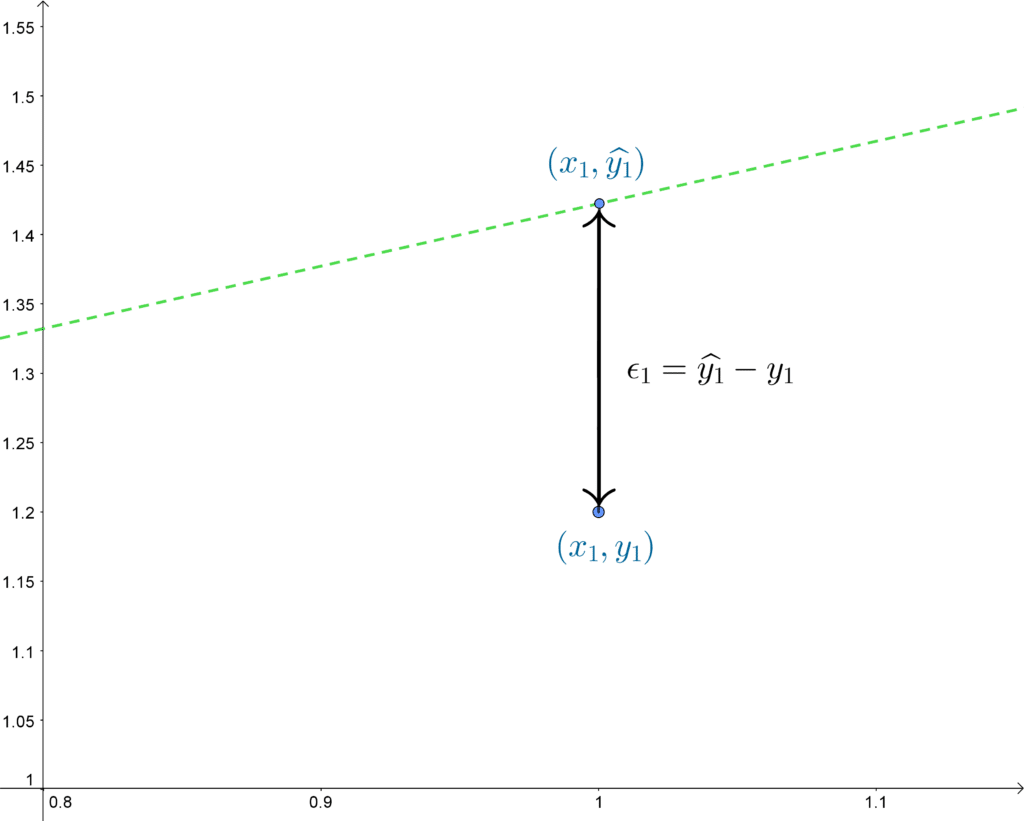
Et avvik εi har vi for alle punktene, med mindre den predikerte og observerte y-verdien sammenfaller, altså at linjen går gjennom punktet.
Denne feilen kan enten ha positiv eller negativ verdi. Fortegnet vil avhenge av om den ekte y-verdien ligger over eller under vår anslåtte y-verdi. Men vi er jo interessert i å ha minst mulig feil, uavhengig av fortegnet. La oss derfor kvadrere dette slik at det alltid blir positivt. Det er akkurat dette minste kvadraters metode baserer seg på. Anslagsfeilene kvadreres i alle punkter og legges sammen. Derav navnet minste kvadraters metode.
Sum\space av\space kvadrat\space av\space feil =\sum^{n}_{i=1}\epsilon_i^2=\sum^{n}_{i=1}\left( \hat{y}_i-y_i \right)^2Summen av alle de kvadrerte feilene ønsker vi å minimere. Denne minimeringen får vi til ved å løse de to ligningene under:
1)\space\space\space \frac{\partial}{\partial\alpha}\space\sum^{n}_{i=1}\left( \hat{y}_i-y_i \right)^2=0 \newline
2)\space\space\space \frac{\partial}{\partial\beta}\space\sum^{n}_{i=1}\left( \hat{y}_i-y_i \right)^2=0Resultatet av minste kvadraters metode – regresjonsparametere
Det er en ganske komplisert og unødvendig prosess å regne ut de to ligningene når andre allerede har gjort det, så vi kan gå rett til resultatet.
Koeffisientene som gir lavest sum av kvadrerte anslagsfeil er:
\hat{b}=\frac{S_{xy}}{S_{xx}}=
\frac{\sum^{n}_{i=1}\left( x_i-\bar{x} \right) \left( y_i-\bar{y} \right)}{\sum^{n}_{i=1}\left( x_i-\bar{x} \right)^2}
\\~\\
\hat{\alpha}=\bar{y}-\hat{\beta}\bar{x}De ulike symbolene i formlene over er:
\bar{x}\text{, } \bar{y}:\text{ gjennomsnitt til } x \text{ og } y\space\space\space\space
\\
S_{xx}: \text{variansen til x}\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space
\\
S_{xy}: \text{kovariansen mellom } x \text{ og } yHåper dette ga deg en oppklaring i hva minste kvadraters metode er for noe og at du føler deg klar til å prøve litt på egenhånd. Dersom du ønsker å lære mer om statistikk, så test ut våre kurs på EnkelEksamen.




