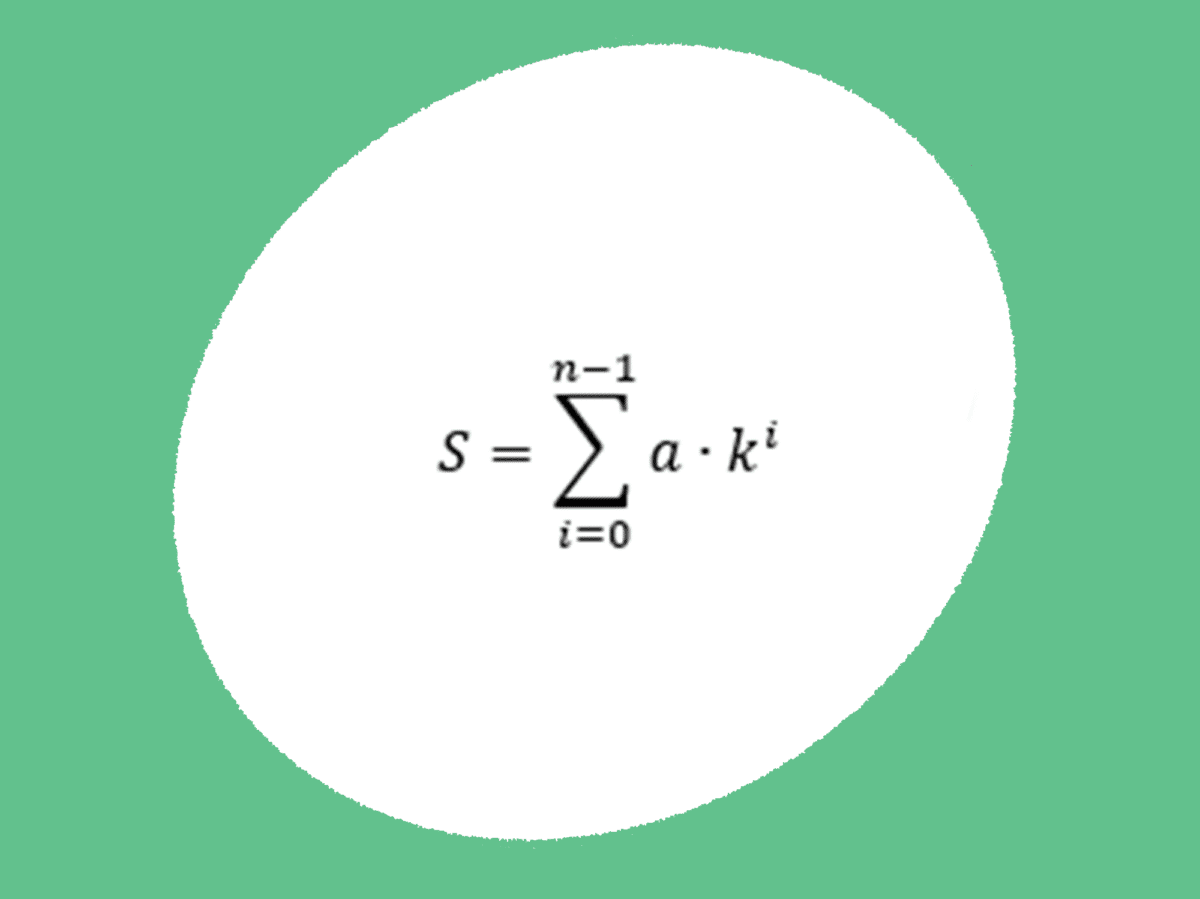Det sies at derivasjon er et verktøy, mens integrasjon er en kunst. Derfor er det kanskje ikke så rart at integrasjon fort kan gi hodebry. Noen ganger også hodevondt etter at man har dunket hodet hardt i pulten av frustrasjon. Integrasjon er ikke enkelt! Hva er integrasjon? Hvordan integrerer man? Disse spørsmålene blir besvart i denne teksten.
Vi må først lære litt notasjon. Hvis vi skal skrive at vi integrerer en funksjon f(x), så skriver vi

Her er

tegnet for integrasjon. Vi skal ikke gå inn i dybden på hvorfor vi skriver dx på slutten, men dette er viktig. Det å ikke skrive dx kan sies å være en dødssynd i matematikken (dette er ikke tull, integrasjon uten å skrive dx gjøres på eget ansvar. Du kan ende opp med noen harde slag med linjal i bakhodet).
Hva er integrasjon?
La oss tenke oss at du har en funksjon f(x) og du ønsker å finne arealet mellom grafen og x-aksen. Hva er den beste fremgangsmetoden?

Du kan jo starte med å tegne noen rektangler. Bredden i rektanglene er den samme, men høyden til rektangelet er bestemt ut fra verdien til f(x). Vi kan beregne arealet til hvert rektangel og så kan vi ta summen av alle arealene for å få en approksimasjon til arealet under grafen. Vi kan se dette på figur 2. En approksimasjon vil si at svaret ikke er eksakt riktig, men at det er i nærheten. Hvis vi øker antallet rektangler vi bruker, slik at bredden til hvert rektangel blir mindre, så vil vi komme nærmere det korrekte svaret. Dette kan vi se på figur 3.


Når vi integrerer så er det som om vi bruker uendelig mange slike rektangler. Da vil vi få beregnet helt nøyaktig arealet under grafen. Et integral gir oss altså arealet under grafen ned til x-aksen. Er funksjonen negativ, så vil integralet gi et negativt svar.
Integrasjon er antiderivasjon
En annen måte å se på integrasjon på, er som det motsatte av derivasjon. Integrasjon er antiderivasjon. Dette medfører at hvis vi har en funksjon F(x) , så deriverer vi funksjonen og får F'(x)=f(x), så er det slik at:

Vi ser at vi ender opp med den samme funksjonen F(x) plusset sammen med et ledd C, hvor C er en konstant. Her ser vi da at integrasjon gjør slik at vi ender opp med samme funksjon vi startet med. Grunnen til at vi må ha med C er fordi når vi deriverer noe, så er det jo slik at konstantledd forsvinner. Derfor må vi ha med +C for å forsikre oss om at vi regner med eventuelle konstantledd.
Bestemt og ubestemt integral
Vi har to ulike typer integraler. Bestemt og ubestemt. Hvis vi har et ubestemt integral av funksjonen f(x), så skriver vi dette som

Grunnen til at det heter ubestemt integral, er fordi vi ikke spesifiserer hvor vi ser på funksjonen.
Et bestemt integral av funksjonen f(x) skriver vi som følgende

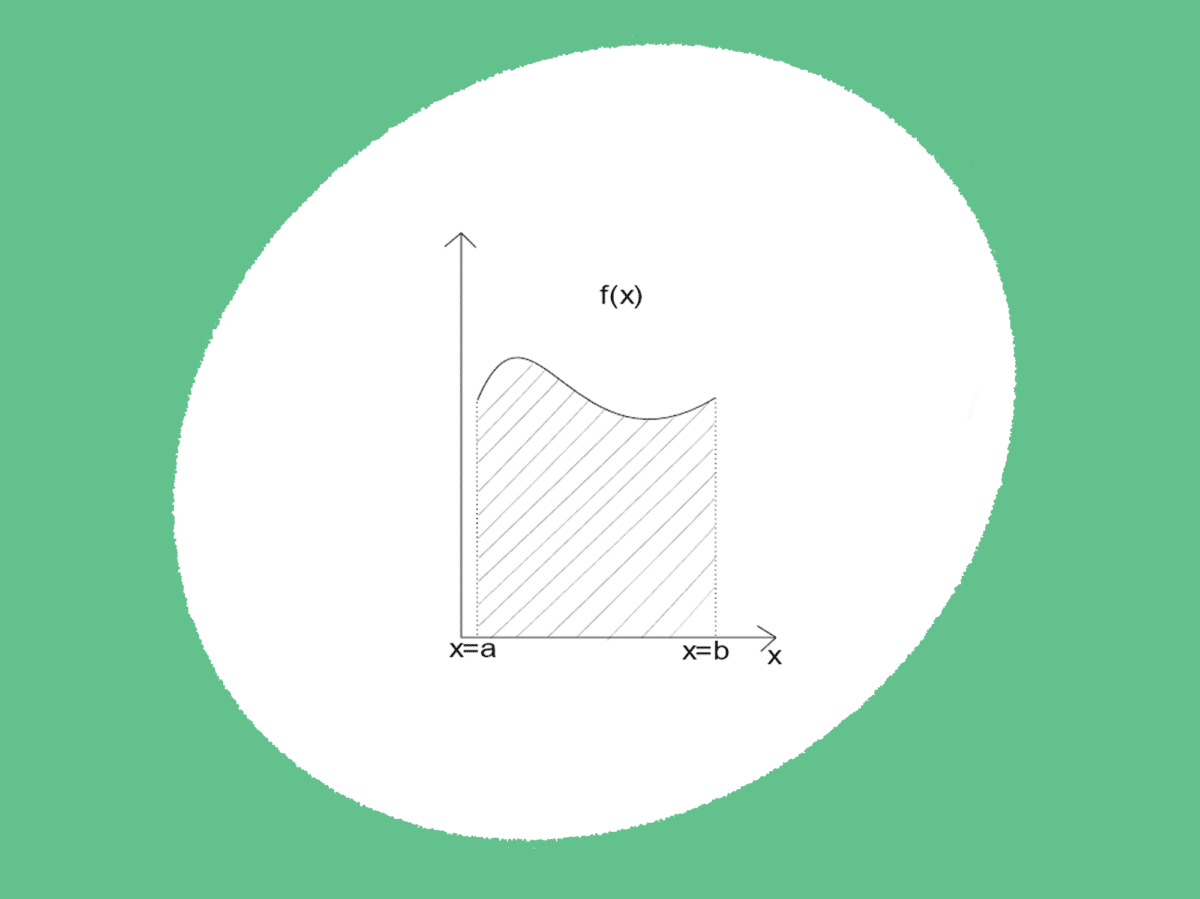
Her har vi spesifisert at vi ser på funksjonen fra x=a til og med x=b. Hvis vi tenker på integraler som noe som gir oss arealet mellom grafen og x-aksen, så vil et ubestemt integral gi oss et generelt svar. Et bestemt integral derimot vil gi oss arealet mellom grafen og x-aksen fra x=a til x=b. Dette kan vi se på figur 4. Her ser vi at vi finner arealet, området som er skravert, mellom x=a og x=b for funksjonen f(x).

Hvordan integrere?
Vi vet at hvis vi har en funksjon

Så er

Som nevnt tidligere i teksten, så er integrasjon det motsatte av derivasjon. Integrasjon er antiderivasjon.
La oss nå si at vi har en funksjon

Da har vi at

Dette gjelder generelt for alle funksjoner på formen

Regneregler for integrasjon

Hvis du har lyst til å lære mer om både integrasjon og mye mer, gå til EnkelEksamen.no og sjekk ut våre matematikkurs. Her finner du gode videoleksjoner som tar deg gjennom alt du trenger fra det mest elementære innen integrasjon, til de aller mest krevende eksamensoppgavene. Du vil også kunne bryne deg på quizoppgaver som tester deg innen alle emnene. Hvis du har noen spørsmål, kan du alltid spørre noen av våre nettlærere 😊