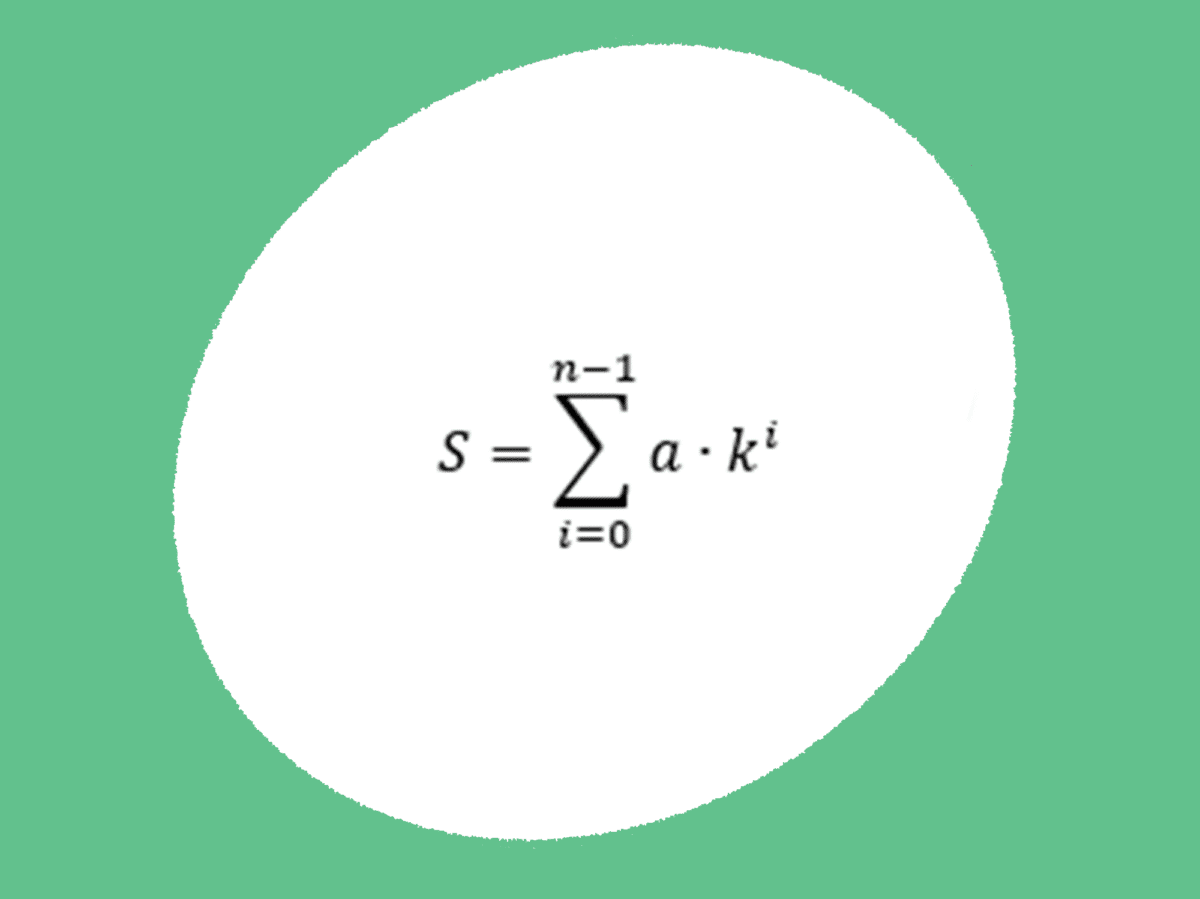En geometrisk rekke, S, er en sum av ledd hvor man finner hvert påfølgende ledd ved å gange det forrige leddet med en gitt konstant som vi kaller kvotienten k. Et eksempel på en geometrisk rekke er som følgende:

Som kan skrives som:

Her er S en geometrisk rekke hvor kvotienten er

Vi kan se at dette stemmer da første leddet er 1, og vi får hvert påfølgende leddene ved å gange det forrige leddet med 1/2
Ergo er

Vi kan uttrykke en geometrisk rekke på følgende vis:

Her er a det første leddet i rekken, k er kvotienten og n er antall ledd rekken består av. Dette er en ganske tungvint måte å skrive på, så vi uttrykker en geometrisk rekke på følgende vis:

Dette kan virke ganske gresk, spesielt med tanke på at

er den greske bokstaven sigma. Men dette er egentlig ganske greit.


betyr enkelt og greit sum. Altså at vi plusser sammen alle leddene
i=0 betyr at i det første leddet setter vi inn for i=0, deretter i=1, osv
n-1 betyr at vi stopper når i=n-1. Ergo vi plusser sammen alle leddene fra og med

til og med

Formel for geometrisk rekke
Nå som du har blitt litt kjent med hva en geometrisk rekke er, så er det på tide å bli kjent med hvordan vi regner ut en geometrisk rekke. Vi kunne ha brukt «brute force» og manuelt plusset på hvert ledd. Men det sier kanskje seg selv at dette ikke er den mest effektive fremgangsmetoden. Det finnes en formel for å beregne en geometrisk rekke.
Utledning av formel
Vi har rekken

Nå ganger vi denne rekken med k, og får da

Hvis vi nå trekker fra S fra S*k

På høyre side av likhetstegnet er det slik at alle leddene utenom

og

kanselerer hverandre. Dermed står vi igjen med

På venstre side kan vi nå gjenkjenne at vi har en felles faktor S, og vi faktoriserer

Hvis vi nå deler på (k-1) på begge sider av likhetstegnet, så får vi en generell formel for den geometriske rekken S

Da har vi at formelen for en geometrisk rekke er som følgende:

Eksempel på utregning

Det første vi gjør er at vi identifiserer a, k og n. Vi har at det første leddet i rekken er 1, altså er a=1. Deretter ser vi at vi får de påfølgende leddene ved å gange det forrige leddet med 1.01, altså er k=1.01. Vi ser at det siste leddet er

altså er er n-1=32, dermed er n=33.
Nå kan vi benytte oss av formelen

Vi setter inn for a, k og n

Da har vi enkelt og greit funnet verdien av den geometriske rekken S
Uendelig geometrisk rekke
Det kan hende at du støter på oppgaver som ber deg om å beregne en geometrisk rekke, når antall ledd rekken består av går mot uendelig. Altså

Hvordan skal du beregne dette? For å finne ut hva en slik geometrisk rekke blir, så må vi starte med å se på konvergens og divergens.
En rekke divergerer hvis den ikke går mot noen spesifikk verdi, men bare vokser og vokser mot enten

eller

Altså en rekke divergerer hvis

Men dette er ikke alltid tilfellet. Vi kan også ha at en rekke konvergerer, altså at rekken går mot en spesifikk verdi. Altså en rekke konvergerer hvis

Hvor c ikke er

Hvordan finne ut om en rekke divergerer eller konvergerer?
Men hvordan kan vi avgjøre om en geometrisk rekke konvergerer eller divergerer? For å avgjøre dette kan vi se på formelen for en geometrisk rekke, og grenseverdien når


Dette kan vi skrive om til

I dette uttrykket er det kun

som er avhengig av n, altså er det k som avgjør om S konvergerer eller divergerer.

Det er slik at hvis |k|<1, altså at -1<k<1, så vil rekken konvergere. Dette er fordi når vi ganger et tall som er i absoluttverdi mindre enn 1 med seg selv, så vil produktet bli mindre. Dermed vil det være slik at hvis |k|<1, så vil

Dermed vil rekken konvergere mot en spesifikk verdi.
Hvis |k|>1 derimot, da vil den geometriske rekken divergere. Dette er fordi et tall som er i absoluttverdi større enn 1 ganget med seg selv, vil bli større og større. Dermed vil S bare vokse og vokse i det uendelige. Da har vi altså et konvergenskrav for geometriske rekker. Rekken konvergerer hvis |k|<1. Hvis |k|<1 og vi har at

så kan vi skrive om formelen for den geometriske rekken til å bli

Dette kan skrives om til

Hvis du trenger mer hjelp med rekker og andre konsepter innen matematikk, ta deg en tur inn på enkeleksamen.no og sjekk ut våre matematikkurs da vel! Hos EnkelEksamen har vi videoleksjoner som går gjennom alt stoffet du trenger til eksamen og quizer du kan bruke til å øve og teste deg selv, og hvis du lurer på noe som helst kan du alltids spørre noen av oss nettlærere😊