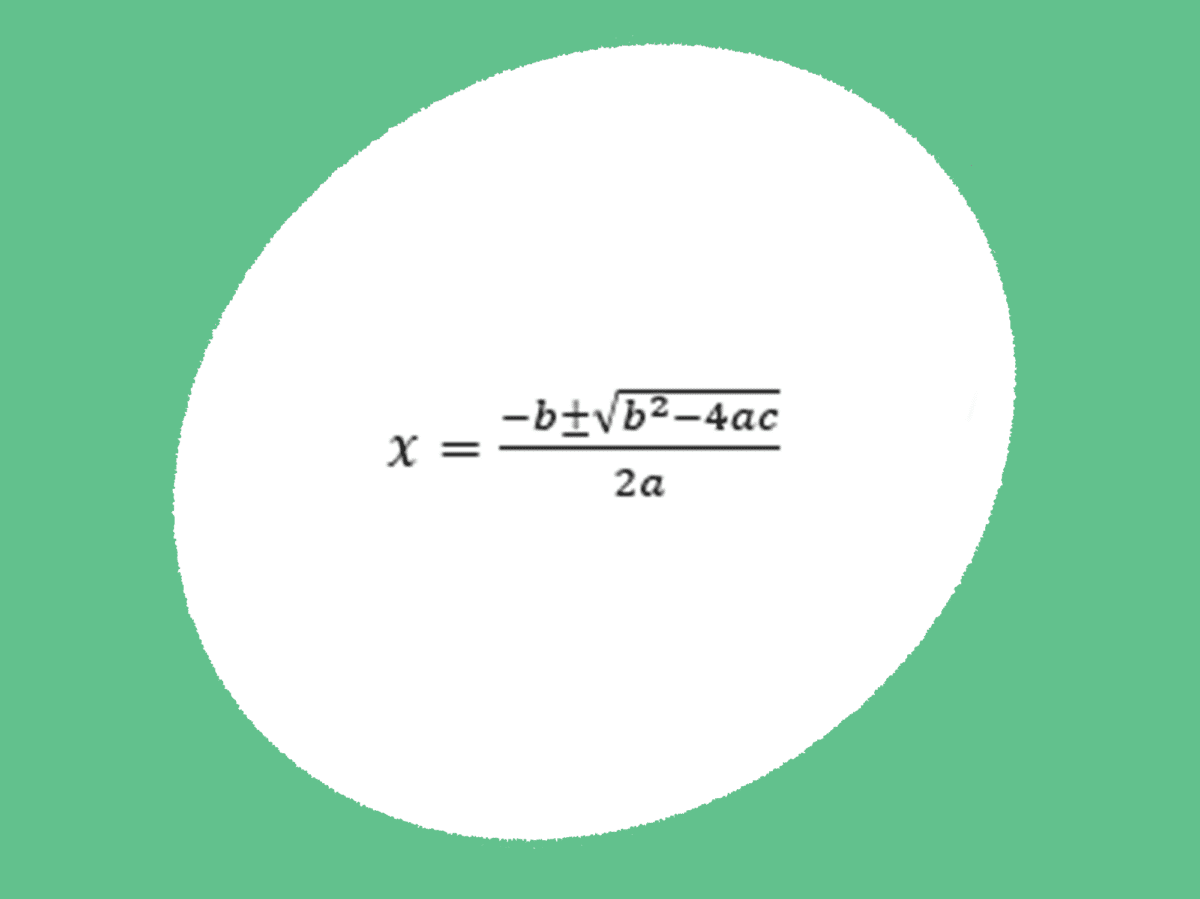I denne teksten skal vi sammen gå gjennom hva ABC-formelen er for noe. Vi skal se på hvordan du regner oppgaver som spør deg om å løse andregradsligninger, samt hvordan vi finner nullpunkter til funksjoner.
ABC-formelen
Kanskje noen har sagt at du må bruke ABC-formelen, men hva er det for noe? Du har sikkert støtt borti en oppgave som spør deg om løse noe som:

Men hvordan gjør man egentlig dette?
Vi kan starte med å se litt på hva ABC-formelen egentlig er for noe. Du kan tenke på ABC-formelen som et verktøy som du kan benytte deg av for å løse andregradsligninger. En generell andregradsligning ser ut som dette:

Her er x en variabel, altså x kan ha flere mulige verdier og kan variere, mens a, b og c er konstanter og vil ha en spesifikk verdi. La oss se på et eksempel:

I dette eksempelet vil a=1 , b=9 og c= -22. Vi kan alltid skrive andregradsligninger på denne formen, men dette krever kanskje litt forandring av det originale uttrykket. Hvis vi har et uttrykk som ser ut som dette:

På begge sider av likhetstegnet kan vi trekke ifra

Da får vi:

Nå ser vi at vi har

Men hva har andregradsligninger som dette med ABC-formelen å gjøre?
Bruke ABC-formelen til å løse andregradsligninger
Det som er så fint med ABC-formelen er at den hjelper oss med å løse andregradsligninger som er på formen

ABC-formelen gir oss hva x må være for at et annengradsuttrykk skal være lik null. Formelen benytter seg av konstantene a, b og c for å avgjøre hva x må være.
La oss se litt på ABC-formelen

Vi ser fra formelen at vi får hva x må være, og vi ser at vi bruker a, b og c for å avgjøre dette.
La oss se på et eksempel

Nå kan vi bruke ABC-formelen, og vi har at a=1, b=9 og c=-22 , så vi får følgende tall i formelen:

Så kan vi regne ut for hvilke verdier x-verdier som gir


Eller

Vi får altså to løsninger på ligningen; x=2 og x=-11
Vi må ha med begge løsningene, da begge -verdiene gir oss en løsning på ligningen. Hvis vi bare tar med en av løsningene, så har vi ignorert en annen, gyldig løsning. Hvis vi ser på grafen under, så ser vi grafen for

Der hvor grafen krysser x-aksen, vil vi ha løsninger på ligningen .

Vi ser fra grafen at dette er tilfellet når x=2 og x=-11, akkurat som vi beregnet.

Eksempel: hvordan løse andregradsligning
Vi kan prøve å løse

Vi starter med å gjøre om uttrykket slik at vi får 0 på ene siden.
Derfor trekker vi fra (-6x+1) på begge sider av likhetstegnet:

Nå bruker vi ABC-formelen

på uttrykket

Vi har at a=1, b=3 og c= -4. Setter vi det inn i formelen får vi:

Nå regner vi ut hva dette er for noe:

Altså vil

Når x=1 eller når x= -4. Da har vi løst denne annengradslingningen ved hjelp av ABC-formelen. Vi kan under se grafen til både

og


Vi kan se at de to grafene krysser hverandre i to punkter, der hvor x= -4 og x=1 . Der hvor grafene krysser hverandre vil

og vi ser at dette passer med hva vi har beregnet.
Funksjoner: regne ut nullpunkter med ABC-formelen
Du har kanskje støtt borti noen oppgaver hvor du må finne nullpunkter til funksjoner. Her kan man også benytte seg av ABC-formelen. Hvis funksjonen ser ut på følgende vis

Så kan vi finne nullpunktene ved å se på følgende 2. gradsligning:

x-verdiene som løser denne andregradsligningen vil også resultere i at funksjonen f(x)=0 . Dermed kan vi finne nullpunkter for ulike funksjoner ved hjelp av ABC-formelen. La oss se på et eksempel

Hva er nullpunktene?
Det første vi kan gjøre for å finne nullpunktene til f er at vi kan skrive om funksjonsuttrykket litt, da det er slik at x er felles faktor for alle leddene, og dermed kan vi skrive f som

Nå kan vi finne nullpunktene. Først og fremst kan vi se at f blir lik null når x=0. Dette kommer av at null ganger noe er lik null. Men nå kan vi finne de resterende nullpunktene ved å finne ut når

Nå må vi benytte oss av ABC-formelen. Vi har at a=1, b= -4 og c=4

Da har vi altså at f(x)=0 når x=0 eller x=2 . For slike problemer, så er det viktig at vi svarer med alle mulige løsninger. Her ville det ikke vært et fullstendig svar hvis vi bare hadde svart x=0 for eksempel. Det er riktig at f(0)=0 , men vi har også at f(2)=0. Så vi hadde ignorert en løsning hvis vi bare hadde tatt med enten x=0 eller x=2.
Under kan du se grafen til f(x). Du kan se at grafen til f treffer x-aksen når x=0 og x=2 . Dette tilsvarer nullpunktene til f(x).

Hvis du trenger mer hjelp med andregradsligninger og andre konsepter innen matematikk, ta deg en tur inn på enkeleksamen.no og sjekk ut våre matematikkurs da vel! Hos enkeleksamen har vi videoleksjoner som går gjennom alt stoffet du trenger til eksamen og quizer du kan bruke til å øve og teste deg selv. Hvis du lurer på noe som helst kan du alltids spørre noen av oss nettlærere 😄