Lagrange-metoden er et kraftig verktøy som brukes for å finne maksimum og minimum av funksjoner under gitte betingelser. Enten du studerer matematikk, ingeniørfag, økonomi eller et annet felt som krever avanserte analytiske ferdigheter, kan Lagrange-metoden hjelpe deg med å løse utfordrende problemer med større presisjon og effektivitet. Selv om det kan høres vanskelig ut, er det ikke så ille som mange skal ha det til. Les videre i artikkelen, så skal du få se. 

Hva er lagrange metoden?

Lagrange-metoden er en matematisk teknikk oppkalt etter matematikeren Joseph-Louis Lagrange. Denne metoden hjelper oss med å finne maksimum eller minimum av en funksjon når vi må følge bestemte regler eller begrensninger. 

En praktisk måte å forestille seg Lagrange-metoden på er å tenke på det som at du er på fjelltur og ønsker å finne det høyeste punktet på fjellet. Men du kan ikke gå hvor som helst i terrenget; du må holde deg til en bestemt sti som er tråkket opp. Hva er da det høyeste punktet du kan nå? Lagrange-metoden hjelper oss å finne dette optimale punktet ved å balansere funksjonen vi ønsker å maksimere eller minimere med de begrensningene vi må følge, akkurat som å finne den høyeste toppen langs stien på fjellet.

Lagrangefunksjonen

Lagrange-funksjonen skrives på følgende form. 

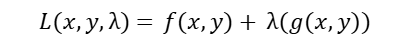
f (x,y) er funksjonen du ønsker å optimalisere, eller fjellet du ønsker å bestige.

g (x,y) er begrensningen du har, eller stien som du er nødt å holde deg på. 

På samme måte som i andre optimaliseringsproblemer, er hovedessensen i Lagrange-metode å sette den deriverte lik null. For å løse optimaliseringsproblemet, partiell-deriverer vi funksjonen med hensyn til hver av de tre variablene og setter dem lik null. Dette gir deg et system av ligninger som kan løses for å finne de optimale verdiene som oppfyller både funksjonen og begrensningene.

Ønsker du å se en video om Lagrange metoden, trykk på denne linken!

Et enkelt eksempel!

Oppsummering

Lagrange-metoden er en kraftig teknikk for å finne optimale løsninger innenfor visse begrensninger. Den brukes i mange ulike fagområder og kan hjelpe oss med å løse komplekse problemer på en strukturert måte. Ved å forstå og anvende denne metoden kan du forbedre din evne til å takle utfordrende analytiske oppgaver. Prøv å bruke Lagrange-metoden i dine egne studier og se hvordan den kan hjelpe deg å oppnå bedre resultater!

Ønsker du også å forstå hvordan vi kan tolke den rare greske bokstaven lambda kan du også se på det ved å trykke på denne linken!

Vil du resten av kurset i Matematikk for Økonomer, sjekk det ut nedenfor!