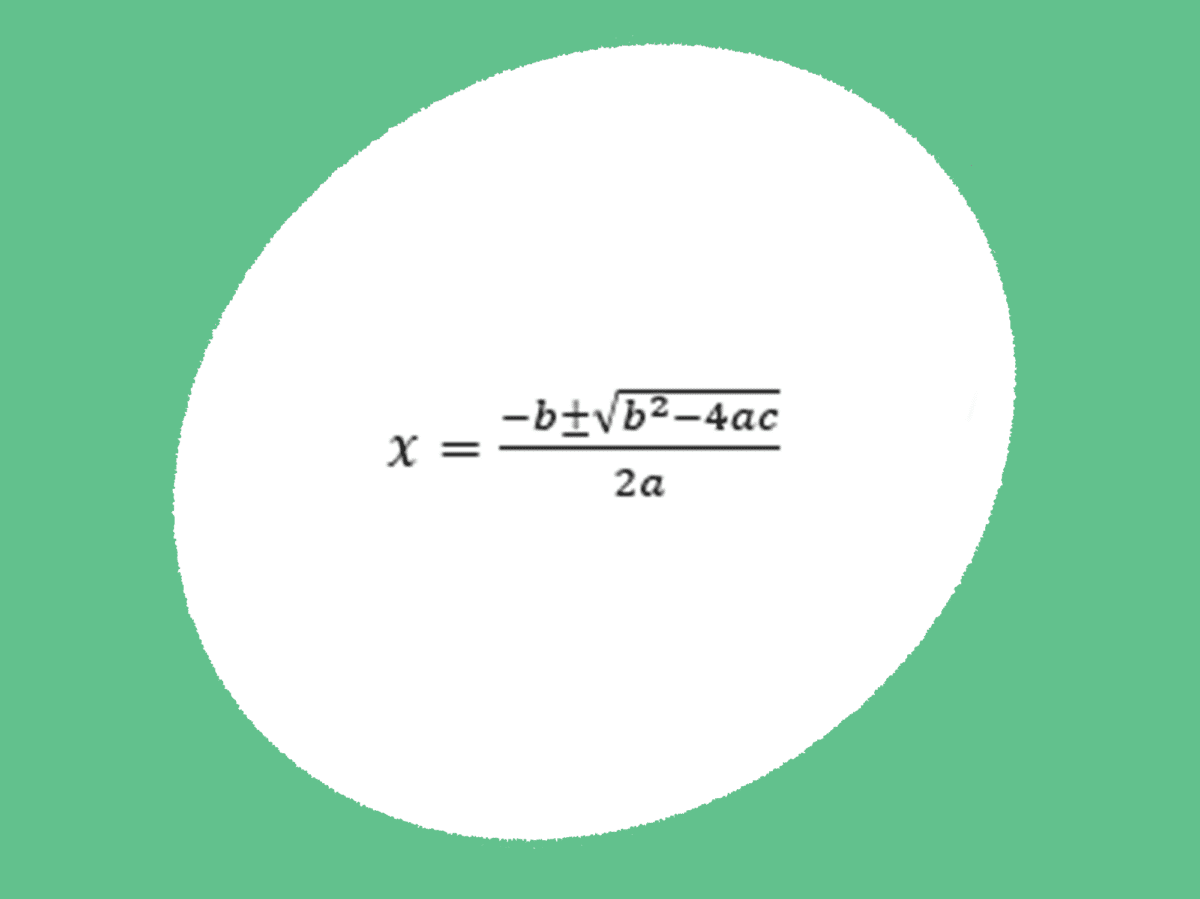I matematikk er funksjoner et svært viktig konsept. Funksjoner tillater oss å modellere ulike systemer og dermed forutsi ulike utfall. Funksjoner er svært viktig innen nesten alle fagfelt, som fysikk, kjemi, biologi, økonomi, etc … Dermed sier det seg selv at det er viktig å forstå hvordan funksjoner oppfører seg. Med andre ord å kunne analysere funksjoner.

Men hva kan du egentlig finne ut om en funksjon og hvordan skal du finne det ut?

Hvis vi har en funksjon f(x), så er det som regel tre punkter vi bryr oss mest om

1. Hvor er f(x) positiv, negativ eller lik null
2. Hvor er f(x) voksende, avtagende eller har et stasjonærpunkt
3. Hvor er f(x) konveks, konkav eller har et vendepunkt

1. Analysere funksjoner: Hvor er f(x) positiv, negativ eller lik null

Hvis vi har denne funksjonen:

så vil grafen se ut som følgende:

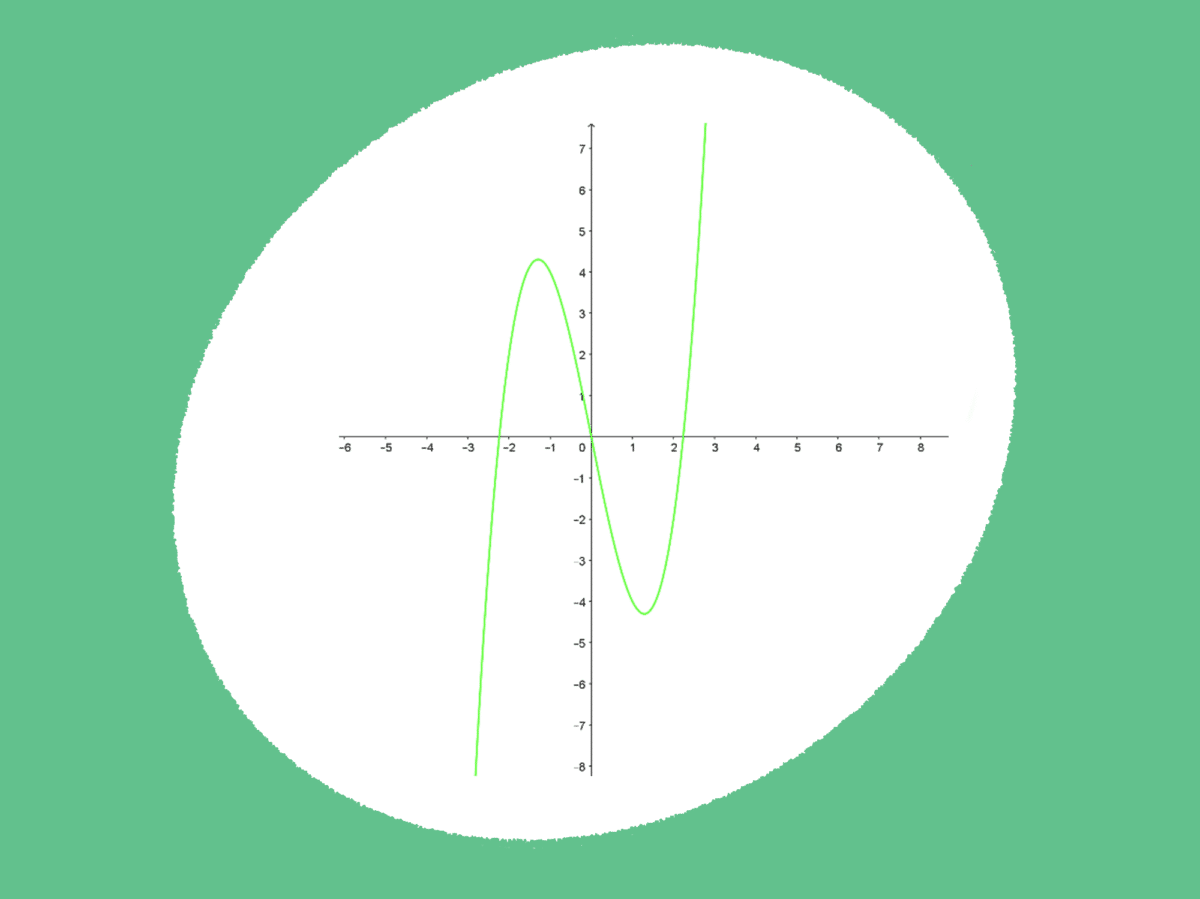
Hvor er f(x) positiv? Hvor er f(x) negativ? Hvor er f(x)=0?

Hvis vi ser på grafen, så er det slik at f(x) er den grønne krummende grafen. f(x) er positiv når den er over x-aksen, hvor x-aksen er den horisontale svarte streken. Hvis grafen til f(x) er under x-aksen, så er f(x) negativ. Når grafen til f(x) treffer x-aksen, så er f(x)=0.

Ved å se på tallene på aksene kan vi se at f(x) er positiv når -2.24<x<0 og 2.24<x. Vi har også at f(x) er negativ når x<-2.24 og 0<x<2.24. Til slutt har vi at f(x)=0 når x=0 eller x=+-2.24. Men hvordan kan vi beregne dette ut fra funksjonsuttrykket? Det er jo som regel slik at oppgaver ber deg beregne dette. For å finne ut når en funksjon er positiv, negativ eller lik null, så benytter vi oss av en fortegnslinje. Vi har at

Du ser kanskje at begge leddene i funksjonsuttrykket har en felles faktor, x. Vi kan skrive funksjonen som

Vi kan også benytte oss av konjugatsetningen, som sier at

Hvis vi sier at

så ser vi at

Da har vi altså at

som vi skriver om til

Nå kan vi lage et fortegnsskjema

Hvis du vil lære hvordan man setter opp fortegnsskjema, så kan du se denne videoen. Fra forttegnskjemaet får vi at f(x) er negativ der den grønne nederste linjen er stiplet. Positiv der den grønne nederste linjen er heltrukken. Og til slutt, f(x)=0 der hvor det er en svart sirkel. Det er slik at

og nå kan du kanskje se at det er disse punktene som ble lest av grafen tidligere i teksten. Dermed har vi funnet når f(x) er positiv, negativ eller lik null.

2. Analysere funksjoner: Hvor er f(x) voksende, avtagende eller har et stasjonærpunkt

Vi kan fortsatt se på denne funksjonen:

Hvordan skal vi beregne når f(x) er voksende, avtagende eller har et stasjonærpunkt? For å finne ut av dette må vi benytte oss av den deriverte. Den deriverte forteller oss den momentane veksten i et gitt punkt for en funksjon. Dermed vil den deriverte til f(x), altså f'(x), si oss hvor funksjonen vokser, avtar eller er konstant. Da kan vi derivere f(x)

Det er slik at verdien f'(c) forteller oss hvor mye f(x) stiger eller synker i punktet x=c. Så for å finne når f(x) vokser eller avtar kan vi lage en forttegnslinje for f'(x). Vi kan først skrive om f'(x) ved å bruke konjugatsetningen. Hvis vi sier at

så får vi

Da får vi at fortegnslinjen blir seende ut som følgende

Den nederste røde linjen, viser når f'(x) er positiv, negativ eller lik null. f'(x) er positiv når linjen er heltrukken, negativ når linjen er stiplet og lik null der hvor det er en svart sirkel. Når f'(x) er positiv, så vokser f(x). Når f'(x) er negativ, så avtar f(x). Hvis f'(x)=0, så har vi et såkalt stasjonærpunkt. I et stasjonærpunkt, vil funksjonen hverken vokse eller avta, så akkurat i dette punktet er funksjonen konstant. Det er slik at hvis den deriverte går fra å være positiv til å bli negativ, vil stasjonærpunktet tilsvare et toppunkt. Hvis den deriverte går fra å være negativ til å bli positiv, vil stasjonærpunktet tilsvare et bunnpunkt. Kan du tenke deg hvorfor dette er tilfellet?

Vanskelig? Eksempel med fjellgåing:

Når den deriverte går fra å være positiv til å bli negativ, så er det slik at funksjonen går fra å stige til å synke.

Tenk deg at du skal gå opp og ned et fjell. Vi kan tenke på hvor høyt oppe du er som en funksjon h. Når du går oppover tilsvarer dette at den deriverte til h er positiv, da h vokser. Toppen vil tilsvare et stasjonærpunkt. Når du begynner å gå nedover igjen, vil h avta og dette tilsvarer at den deriverte av h er negativ. Da forstår vi altså at når den deriverte går fra å være positiv til å være negativ at vi får et toppunkt. På samme vis kan vi forstå at hvis den deriverte går fra å være negativ til å være positiv, så vil vi ha et bunnpunkt. Dette eksemplet kan være nyttig å ha med seg når du skal analysere funksjoner.

Fra fortegnslinjen finner vi da altså at f(x) vokser når x<-1.29 og x>1.29. I tillegg vil f(x) avta når -1.29<x<1.29. Vi har at f(x) har stasjonære punkter for x=-1.29 og x=1.29. Siden den deriverte av f går fra positiv til negativ når x går fra å være mindre enn -1.29 til større enn 1.29, så vil f(-1.29) være et toppunkt for f(x). Siden den deriverte av f går fra negativ til positiv når x går fra å være mindre enn 1.29 til større enn 1.29, så vil f(1.29) være et bunnpunkt for f(x).

3. Analysere funksjoner: Hvor er f(x) konveks, konkav eller har et vendepunkt

Om en funksjon er konveks eller konkav forteller oss om krumningen til funksjonen. Funksjonen er konveks hvis den ser ut som et smilefjes 😊, funksjonen er konkav hvis den ser ut som et trist fjes ☹. Altså er det slik at en konkav funksjon krummer nedover. En konkav funksjon vil ha en avtagende derivert, altså at den deriverte blir mindre og mindre. En konveks funksjon derimot vil ha en voksende derivert, altså vil funksjonen stige raskere og raskere. Hvis en funksjon har et vendepunkt, så vil dette si at funksjonen enten går fra å være konveks til konkav eller konkav til konveks.

Hvordan regne ut dette?

For å finne ut av hvor f(x) er konkav, konveks eller har et vendepunkt, så må vi finne den andrederiverte, f”(x). Den andrederiverte gir oss den momentane vekstfarten til den deriverte. Dette er litt vanskelig å tenke seg, så et enklere vis å forestille seg den andrederiverte på, er at den andrederiverte gir oss krumningen til funksjonen vi ser på. Det er nemlig slik at hvis f”(x)<0, så er f(x) konkav. Hvis f”(x)>0, så er f(x) konveks.

For å finne den andrederiverte, så deriverer vi

Vi har da at f”(x) er negativ når x<0 og positiv når x>0. En funksjon er konkav når f”(x) er negativ, og konveks når f”(x) er positiv. Vi har vendepunkt når f”(x)=0, som her er når x=0. Nå kan vi se på grafen til f(x) for å se at dette stemmer med hvor grafen «smiler» 😊 og hvor grafen er lei seg ☹.

Vi kan her se at grafen ser ut som en trist munn ☹ fram til x=0, og etter x=0 ser grafen ut som en glad munn 😊. Altså er f(x) konkav når x<0 og konveks når x>0. Når x=0 går grafen fra å være konkav ☹ til å være konveks 😊, altså har vi et vendepunkt for x=0.

Lurer du på mer?

Hvis du trenger mer hjelp med funksjonsanalyse og andre konsepter innen matematikk, ta deg en tur inn på enkeleksamen.no og sjekk ut våre matematikkurs da vel! Hos EnkelEksamen har vi videoleksjoner som går gjennom alt stoffet du trenger til eksamen og quizer du kan bruke til å øve og teste deg selv, og hvis du lurer på noe som helst kan du alltids spørre noen av oss nettlærere 😊