Konfidensintervall for forventningsverdi \mu (“my”) blir ofte kalt konfidensintervall for gjennomsnitt. Den riktige formuleringen er at vi bruker gjennomsnitt til å finne et konfidensintervall for parameteren som heter \mu. I dette blogginnlegget skal vi se på hvordan man lager et konfidensintervall for \mu når variansen er kjent og ukjent. Du vil lære å lage konfidensintervall med både z-fordeling og t-fordeling.
Hva er et konfidensintervall
Kort fortalt, så er et konfidensintervall et intervall som vi med høy sikkerhet kan si at inneholder den sanne verdien til en populasjonsparameter. Denne populasjonsparameteren kan for eksempel være forventningsverdien \mu, som vi skal studere i dette blogginnlegget.
Hvor sikre vi er spesifiseres av en variabel kalt \alpha. Hvis \alpha=0,05=5\% så er det snakk om et 95%-konfidensintervall. Dette er en veldig mye brukt verdi for \alpha, men det er fullt mulig at en oppgave ber deg bruke \alpha=0,01, \alpha=0,1 eller noe annet.
Formålet med å finne et konfidensintervall er altså å finne et intervall med en minimumsverdi og maksimumsverdi. Vi er da veldig sikre på at den ukjente variabelen har en verdi som er mellom minimum og maksimum.
\big[\text{minimum},~~ \text{maksimum} \big]Konfidensintervall for vekt på sjokolade

La oss sette opp et eksempel på bruk av konfidensintervall.
En sjokoladeprodusent har begynt å produsere en ny sjokoladebar. Vekten på sjokoladen varierer bittelitt siden ingen maskiner er 100% perfekte til å fylle opp formene. En av arbeiderne ved sjokoladefabrikken er usikker på hvor mye sjokoladene veier. Han ønsker et intervall han er 95% sikker på at inneholder den sanne forventningsverdien for vekten på sjokoladen.
Dette er et utgangspunkt for å lage et konfidensintervall for forventningsverdien \mu.
Skille mellom kjent og ukjent varians
Når vi skal lage konfidensintervall for forventningsverdien, så skiller vi mellom kjent og ukjent varians. Dersom vi vet hvor stor varians det er i f.eks. vekten på sjokoladebarene, så bruker vi normalfordelingen til å finne konfidensintervall. Dersom variansen er ukjent, så kan vi regne ut den empiriske variansen. Hvis vi bruker den empiriske variansen, så må vi bruke t-fordelingen (også kalt Student t-fordeling) til å lage konfidensintervallet.
Nedenfor kan du se fremgangsmåten for å lage et konfidensintervall for vekten på sjokoladebaren, både når variansen er kjent og ukjent.
Bear with me! Her kommer det mye matte og en del av det er litt kronglete å skjønne seg på 🤯 Dette er for å vise hvordan man faktisk kommer frem til formelen for konfidensintervall. Hvis du vil ha formelen er det bare å scrolle nedover, men ta gjerne en titt på matten og se om du skjønner hvorfor formelen er som den er 😃
Konfidensintervall med kjent varians

Lagerarbeideren tar n tilfeldige sjokoladebarer og veier hver enkelt av dem. Vekten på de n sjokoladene er X_1, X_2, ..., X_n. Vi antar at vekten på sjokoladene er uavhengige og normalfordelte med forventningsverdi \mu og varians \sigma^2. I manualen til maskinen som fyller formene finner arbeideren at variansen ved fylling er \sigma^2=4 ~gram^2. Som et estimat for forventningsverdien bruker han gjennomsnittet:
\bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_iSiden X_1, X_2, ..., X_n er uavhengige og normalfordelte så er gjennomsnittet også normalfordelt. Forventningsverdien til \bar{X} er \mu, mens variansen er \sigma^2/n. Dette kan vi skrive som:
\bar{X}\sim N\left(\mu, \frac{\sigma^2}{n}\right)Vi ønsker nå en standard normalfordeling, og kaller denne Z. Måten vi finner en standard normalfordeling er å ta \bar{X} minus forventningsverdien, og dele på standardavviket (roten av variansen).
Z=\frac{\bar{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\sim N\left(0,1\right)I figuren nedenfor er standardnormalfordelingen vist. Vi ønsker å markere to punkter slik at det er \alpha /2 sannsynlighet i hver hale. Da gjenstår det 1-\alpha sannsynlighet i midten. Siden fordelingen er symmetrisk om 0 er disse punktene på \pm z_{\frac{\alpha}{2}}. Disse verdiene er noe man finner i tabeller, så du trenger ikke regne disse selv.
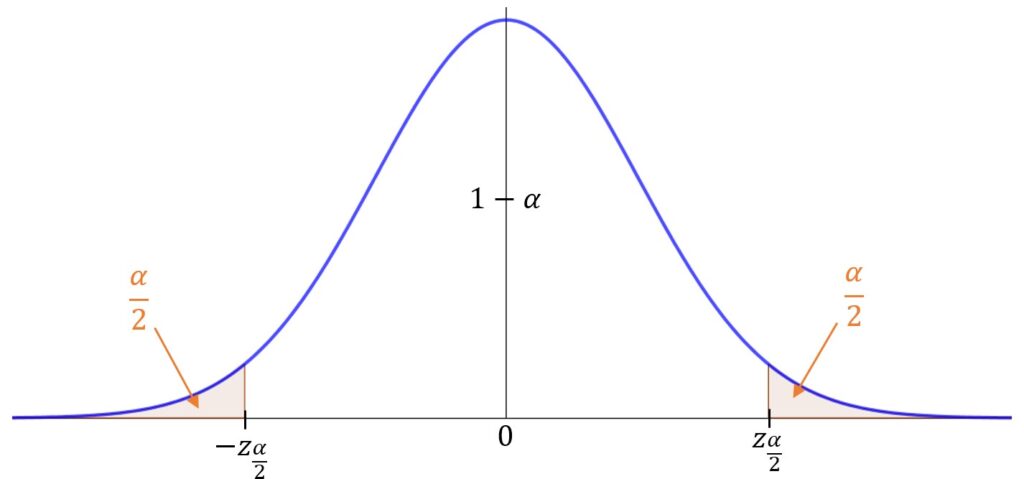
Basert på figuren ovenfor ser vi at sannsynligheten for at Z ligger mellom \pm z_{\frac{\alpha}{2}} er 1-\alpha. Dette kan skrives slik:
P\left(-z_{\frac{\alpha}{2}}\le Z\le z_{\frac{\alpha}{2}}\right)=1-\alpha
\\
\Downarrow
\\
P\left(-z_{\frac{\alpha}{2}}\le \frac{\bar{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\le z_{\frac{\alpha}{2}}\right)=1-\alpha
På det nederste utrykket utføres så tre steg:
- Gang alt inne i sannsynlighetsutrykket med \sqrt{\frac{\sigma^2}{n}}
- Flytt \bar{X} til utsiden av ulikhetstegnene
- Gang med -1 for å få \mu og ikke -\mu i midten
1: Gang alt inne i sannsynlighetsutrykket med \sqrt{\frac{\sigma^2}{n}}:
P\left(-z_{\frac{\alpha}{2}}\le \frac{\bar{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\le z_{\frac{\alpha}{2}}\right)=1-\alpha
\\
\Downarrow
\\
P\left(-z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}~\le~ \bar{X}-\mu~\le~ z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}\right)=1-\alpha2: Flytt \bar{X} til utsiden av ulikhetstegnene
P\left(-z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}~\le~ \bar{X}-\mu~\le~ z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}\right)=1-\alpha
\\
\Downarrow
\\
P\left(-\bar{X}-z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}\le -\mu\le -\bar{X}+ z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}\right)=1-\alpha3: Gang med -1 for å få \mu og ikke -\mu i midten. Når det ganges med -1, så må ulikhetstegnene snus.
P\left(-\bar{X}-z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}\le -\mu\le -\bar{X}+ z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}\right)=1-\alpha
\\
\Downarrow
\\
P\left(\bar{X}+z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}\ge \mu\ge \bar{X}- z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}\right)=1-\alphaHåper du hang med helt hit 😃
Det utrykket vi nå har kommet frem til betyr
“Sannsynligheten for at \mu er større enn \bar{X}-z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}} og samtidig mindre enn \bar{X}+z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}} er 1-\alpha“.
Det er akkurat dette konfidensintervallet er! Vi har funnet en øvre og nedre grense for \mu, som vi er 95\% (\alpha=0,05) sikre på at \mu befinner seg innenfor. Formelen for konfidensintervall kan da settes opp som følgende intervall:
\left[ \bar{X}-z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}},~~\bar{X}+z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}} \right]Eller skrevet enda enklere:
\bar{X} \pm z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}Med tallverdier
La oss sette inn noen tallverdier for å få et intervall som ikke bare er matematiske symboler. Arbeideren veier 8 tilfeldige sjokoladebarer og resultatet er vist i tabellen under (målt i gram).
| x_1 | x_2 | x_3 | x_4 | x_5 | x_6 | x_7 | x_8 |
| 48,4 | 51,0 | 49,7 | 48,5 | 54,2 | 53,1 | 48,9 | 49,3 |
Grunnen til at det brukes små x-er her er fordi de er tilknyttet tallverdier. Ofte bruker man store bokstaver når man regner med generelle stokastiske/tilfeldige variabler, som vi gjorde ovenfor. Når vi har tallverdier å knytte til variablene, så brukes ofte små bokstaver.
Gjennomsnittet er \bar{x}=50,4, og vi ønsker å finne et 95% konfidensintervall for \mu, som betyr at vi må bruke \alpha=0,05. Fra før vet vi at variansen er \sigma^2=4. Det siste vi må finne for konfidensintervallet er z_{\frac{\alpha}{2}}=z_{\frac{0,05}{2}}=z_{0,025}=1,960. Denne verdien finner vi i fraktiltabellen for normalfordelingen ved \alpha=0,025.
På vår dokumentside kan du finne et dokument for fraktiltabell -normalkurven.
Da er vi klare til å sette opp konfidensintervallet:
\left[ \bar{x}-z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}},~~\bar{x}+z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}} \right]
\\
\Downarrow
\\
\left[ 50,4-1,960\sqrt{\frac{4}{8}}~,~~50,4+1,960\sqrt{\frac{4}{8}} \right]
\\~
\\
\left[ 50,4-1,39~~,~~50,4+1,39 \right]
\\~
\\
\left[ 49,01~~,~~51,79 \right]Arbeideren kan altså være 95% sikker på at forventningsverdien for vekten på sjokoladen ligger i intervallet \left[ 49,01~,~51,79 \right], når han vet at variansen er \sigma^2=4.
Konfidensintervall med ukjent varians
I forrige seksjon antok vi at variansen var kjent. I eksempelet så sto det i manualen til maskinen at variansen er \sigma^2=4 ~gram^2. Dersom det ikke er oppgitt må vi regne ut variansen til utvalget vårt. Dette kalles empirisk varians (S^2), og regnes ut i fra vekten på de utvalgte sjokoladebarene. For å lese mer om empirisk varians kan du se her. Når variansen var kjent så lagde vi en standardnormalfordelt variabel Z. Siden variansen ikke er kjent vil ikke denne være normalfordel men heller t-fordelt. Denne variabelen kaller vi T:
T=\frac{\bar{X}-\mu}{\sqrt{\frac{S^2}{n}}}\sim t_{n-1}T er t-fordelt med n-1 frihetsgrader. Antall frihetsgrader blir relevant når vi skal finne t_{\frac{\alpha}{2},n-1}, som tilsvarer z_{\frac{\alpha}{2}} fra i stad.
Disse t-verdiene er vist i figuren nedenfor.
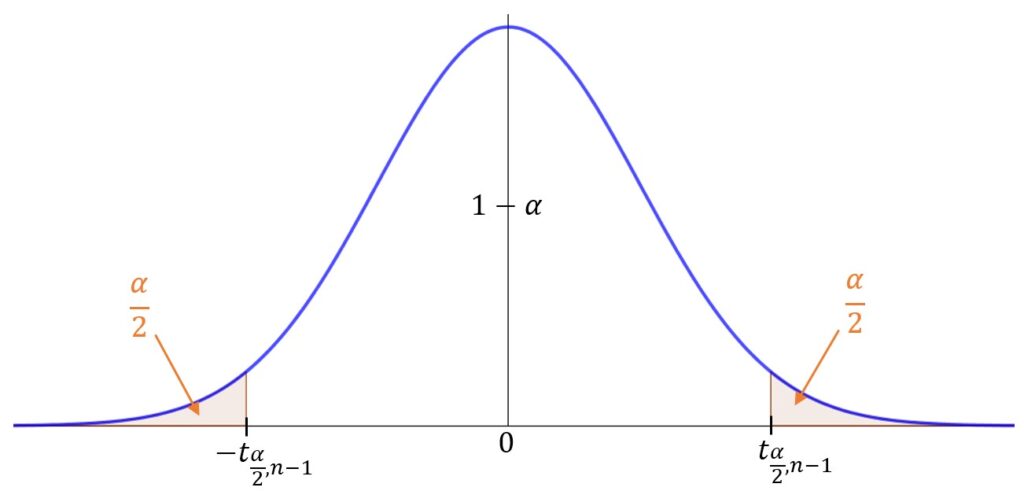
Resten av fremgangsmåten er som med kjent varians, bare med t_{\frac{\alpha}{2},n-1} for z_{\frac{\alpha}{2}} og S^2 for \sigma^2.
Til slutt vil du finne at intervallet blir:
\left[ \bar{X}-t_{\frac{\alpha}{2},n-1}\sqrt{\frac{S^2}{n}},~~\bar{X}+t_{\frac{\alpha}{2},n-1}\sqrt{\frac{S^2}{n}} \right]Eller skrevet enda enklere:
\bar{X} \pm t_{\frac{\alpha}{2},n-1}\sqrt{\frac{S^2}{n}}Med tallverdier
Vi bruker samme tallverdier som tidligere:
| x_1 | x_2 | x_3 | x_4 | x_5 | x_6 | x_7 | x_8 |
| 48,4 | 51,0 | 49,7 | 48,5 | 54,2 | 53,1 | 48,9 | 49,3 |
Gjennomsnittet er fortsatt \bar{x}=50,4. Nå trenger vi den empiriske variansen:
\begin{aligned}
S^2=&\frac{1}{n-1}\sum_{i=1}^{n}\left(x_i-\bar{x}\right)^2
\\
\approx& 4,82
\end{aligned}Som tidligere ønsker vi å finne et 95% konfidensintervall for \mu, som betyr at vi må bruke \alpha=0,05. Det siste vi må finne for konfidensintervallet er t_{\frac{\alpha}{2},n-1}=t_{\frac{0,05}{2},8-1}=t_{0,025, ~7}=2,365. Denne verdien finner vi i fraktiltabellen for t-fordelingen ved \alpha=0,025 og df=7. “df” (degrees of freedom”) er antall frihetsgrader.
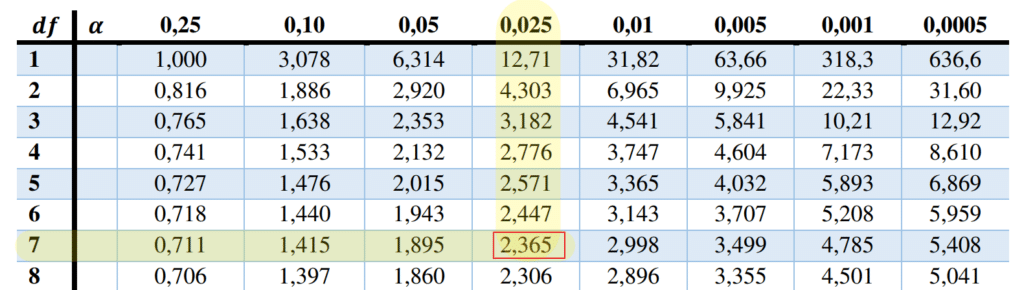
På vår dokumentside finner du også et dokument for T-tabell – Statistikk.
Da er vi klare til å sette opp konfidensintervallet:
\left[ \bar{x}-t_{\frac{\alpha}{2},n-1}\sqrt{\frac{S^2}{n}},~~\bar{x}+t_{\frac{\alpha}{2},n-1}\sqrt{\frac{S^2}{n}} \right]
\\
\Downarrow
\\
\left[ 50,4-2,365\sqrt{\frac{4,82}{8}}~,~~50,4+2,365\sqrt{\frac{4,82}{8}} \right]
\\~
\\
\left[ 50,4-1,84~~,~~50,4+1,84 \right]
\\~
\\
\left[ 48,56~~,~~52,24 \right]Arbeideren kan altså være 95% sikker på at forventningsverdien for vekten på sjokoladen ligger i intervallet \left[ 48,56~,~52,24 \right], når han ikke kjenner til variansen.
Da håper jeg du hang med på gjennomgangen 😅
Om du ønsker å bli en skikkelig mester i statistikk så sjekk ut våre kurs Statistikk og Statistikk for økonomer på enkeleksamen.no. Her har du mulighet til å lene deg tilbake og se flere timer video, i tillegg til å gjøre quizzer!




