Derivasjonsregler og derivasjon

Du har kanskje støtt borti oppgaver eller problemer som spør om den deriverte, men hva vil det si å derivere? Hvordan var det med disse derivasjonsreglene? Hva kan man bruke den deriverte til? Og kanskje viktigst av alt, hvordan regner man ut den deriverte?

Denne teksten vil prøve å besvare disse spørsmålene, og gi deg oversikt og kontroll på derivasjonsreglene. Trenger du mer innføring i derivasjon kan du gå til EnkelEksamen.no og sjekke ut våre matematikkurs.

Hva er egentlig derivasjon?

Den deriverte kan sies å være

1. Den momentane vekstraten til funksjonen f(x)
2. Stigningstallet til tangenten til funksjonen f(x) i punktet x

(Hervik, 2020, 2. avsnitt).

Det vi mener med «Den momentane vekstrater til funksjonen f(x)» er at den deriverte sier hvor fort funksjonen f(x) stiger eller synker i ett punkt.

Det vi mener med at den deriverte er «stigningstallet til tangenten til funksjonen f(x) i punktet x» er at vi kan tegne en rett linje som tangerer funksjonen i et punkt x. Hvor mye denne rette linjen stiger eller synker, altså stigningstallet til den rette linjen, er den deriverte.

Eksempel på derivasjon

La oss se på et lite eksempel på dette. Vi har en funksjon:

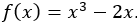
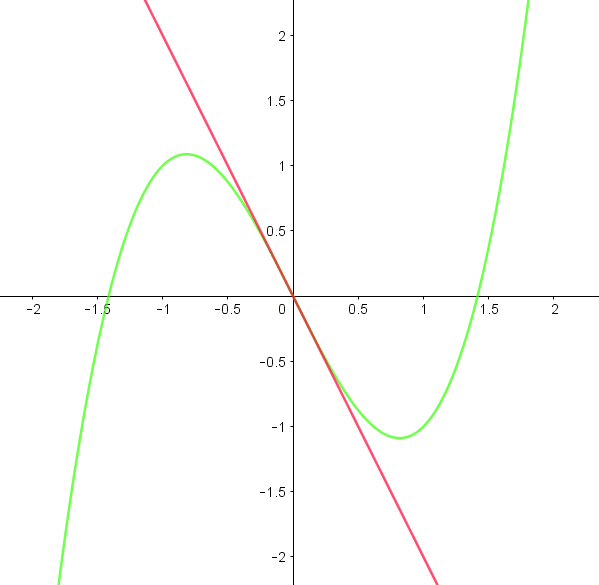
Nå vil vi vite hvor fort f(x) synker når x=0. Hvis du ser på Figur 1, så ser du en grønn svingende graf, dette er grafen til f(x). Du vil også se en rett, rød graf, dette er grafen for tangenten til f(x) i punktet x=0. Stigningstallet til den røde rette grafen, er hvor mye f(x) minker i punktet x=0. Stigningstallet til den røde rette grafen er den deriverte til f når x=0.

Den deriverte forteller oss altså om en funksjon stiger eller synker, og hvor mye funksjonen stiger eller synker. Dette er veldig nyttig for å analysere funksjoner. La oss tenke oss at vi har en funksjon, h , som beskriver hvor høyt opp et fjell du er. Her vil den deriverte til h si hvor bratt opp eller ned det er, der hvor du står. På toppen av fjellet vil det ikke være noe stigning eller synking, og den deriverte er lik null.

Vi kan altså med den deriverte avgjøre om du er på vei opp, ned eller om du er på toppen. Hvis du er på vei oppover vil den deriverte være positiv siden funksjonen h øker, hvis du er på vei nedover vil den deriverte være negativ siden funksjonen h minker. Befinner du deg på toppen, så vil den deriverte være lik null. Dette kan vi se på den følgende grafen.

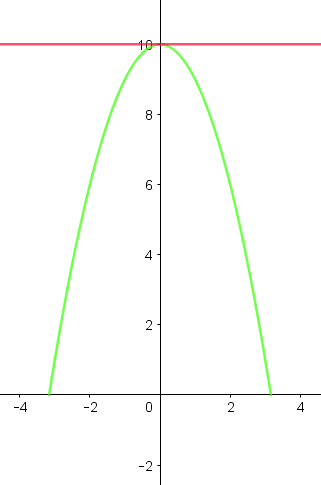
Hvis vi tenker at den grønne, krumme grafen er h, så er den røde rette linjen tangenten til h der hvor h er høyest. Vi ser at tangenten hverken stiger eller synker, så derfor er den deriverte lik null.

Hva bruker vi den deriverte til?

Vi kan bruke den deriverte til å avgjøre om en funksjon stiger eller synker. Den deriverte forteller også hvor mye en funksjon stiger eller synker. I tillegg forteller den deriverte oss hvor en funksjon er på sitt høyeste eller laveste punkt. En funksjon stiger hvis den deriverte er positiv. En funksjon minker hvis den deriverte er negativ. Hvis den deriverte er lik null, så er funksjonen enten på et av sine høyeste punkt, eller et av sine laveste punkt.

Vi skriver den deriverte av  på følgende vis:

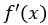
Apostrofen indikerer at vi har derivert funksjonen.

Nå kan vi se litt på noen derivasjonsregler og hvordan man beregner den deriverte til ulike funksjoner.

Derivasjon av potensfunksjon:

En potensfunksjon ser slik ut:

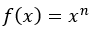
Den deriverte av funksjonen blir:

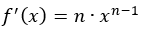
Eksempel: hvordan derivere potensfunksjon

Tenk deg funksjonen:

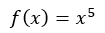
Den deriverte blir da

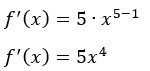
Derivasjon av konstant:

Hvis vi prøver å derivere en konstant, så får vi null.

Funksjonen

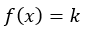
Medfører at

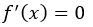
Dette gir mening da den deriverte gir oss hvor mye en funksjon stiger eller synker. Siden en konstant er konstant, så vil ikke denne hverken stige eller synke og den deriverte blir dermed lik null.

Eksempel: hvordan derivere en konstant

Du har funksjonen:

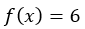
Da er den deriverte:

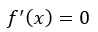
Derivasjon av brøk:

Det kan være nyttig å vite at en brøk kan gjøres om:

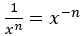
Etter å ha gjort dette kan du igjen bruke regelen for derivasjon av potenser

Eksempel: hvordan derivere en brøk

Har du dermed en brøk, gjør du den først om til en potensfunksjon:

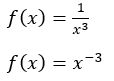
Dermed kan du regne ut den deriverte slik:

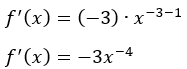
Under følger en tabell med regneregler for derivasjon:

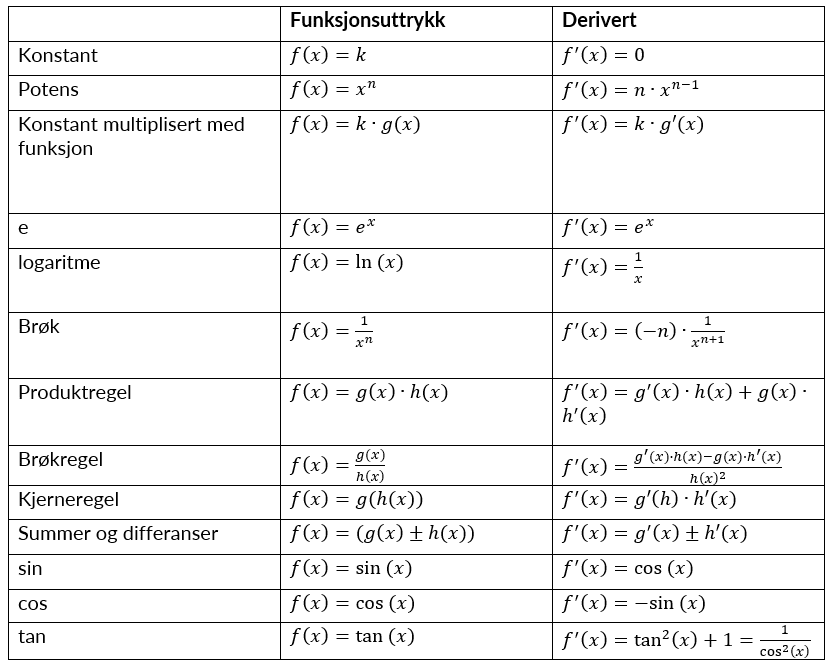
Kilder:

Hervik, Sigbjørn (2020): derivasjon – matematikk i Store norske leksikon på snl.no. Tilgjengelig fra http://snl.no/derivasjon_-_matematikk (Hentet: 14. juli 2020)